
ЁОЬтФПЁП(1)ШчЭМЃЌACЦНЗжЁЯDABЃЌЁЯ1=ЁЯ2ЃЌЪдЫЕУїABгыCDЕФЮЛжУЙиЯЕЃЌВЂгшвджЄУїЃЛ
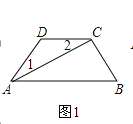
(2)ШчЭМЃЌABЁЮCDЃЌABЕФЯТЗНСНЕуEЁЂFТњзу:BFЦНЗжЁЯABEЁЂDFЦНЗжЁЯCDEЃЌШєЁЯDFB=20ЁуЃЌЁЯCDE=70ЁуЃЌЧѓЁЯABEЕФЖШЪ§ЃЛ
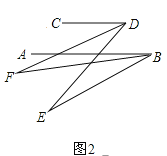
(3)дкЧАУцЕФЬѕМўЯТЃЌШєPЪЧBEЩЯвЛЕуЃЌGЪЧCDЩЯШЮвЛЕуЃЌPQЦНЗжЁЯBPGЃЌPQЁЮGNЃЌGMЦНЗжЁЯDGPЃЌЯТСаНсТл:ЂйЁЯDGP-ЁЯMGNЕФжЕВЛБфЃЛЂкЁЯMGNЕФЖШЪ§ВЛБфЃЌПЩвджЄУїжЛгавЛИіЪЧе§ШЗЕФЃЌЧыФузїГіе§ШЗЕФбЁдёВЂЧѓжЕ.

ЁОД№АИЁПЃЈ1ЃЉABЁЮCDЃЛЃЈ2ЃЉЁЯABE=30ЁуЃЛЃЈ3ЃЉЂкЁЯMGNЕФЖШЪ§ЮЊ15ЁуВЛБфЃЌжЄУїМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнФкДэНЧЯрЕШЃЌСНжБЯпЦНаажЄУїМДПЩЃЛ
ЃЈ2ЃЉЯШгЩНЧЦНЗжЯпЕФЖЈвхПЩЕУЃКЁЯCDFЃН![]() ЁЯCDE=35ЁуЃЌЁЯABE=2ЁЯABFЃЌШЛКѓИљОнСНжБЯпЦНааФкДэНЧЯрЕШЃЌПЩЕУЃКЁЯ2=ЁЯCDF=35ЁуЃЌШЛКѓРћгУШ§НЧаЮЭтНЧЕФаджЪЧѓГіЁЯABFЕФЖШЪ§ЃЌНјЖјПЩЧѓЁЯABEЕФЖШЪ§ЃЛ
ЁЯCDE=35ЁуЃЌЁЯABE=2ЁЯABFЃЌШЛКѓИљОнСНжБЯпЦНааФкДэНЧЯрЕШЃЌПЩЕУЃКЁЯ2=ЁЯCDF=35ЁуЃЌШЛКѓРћгУШ§НЧаЮЭтНЧЕФаджЪЧѓГіЁЯABFЕФЖШЪ§ЃЌНјЖјПЩЧѓЁЯABEЕФЖШЪ§ЃЛ
ЃЈ3ЃЉИљОнШ§НЧаЮЕФвЛИіЭтНЧЕШгкгыЫќВЛЯрСкЕФСНИіФкНЧЕФКЭПЩЕУЁЯ1=ЁЯBPG+ЁЯBЃЌдйИљОнЦНааЯпЕФаджЪвдМАНЧЦНЗжЯпЕФЖЈвхБэЪОГіЁЯMGPЁЂЁЯDPQЃЌИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУЁЯNGP=ЁЯGPQЃЌШЛКѓСаЪНБэЪОГіЁЯMGN=![]() ЁЯBЃЌДгЖјХаЖЈЂке§ШЗЃЎ
ЁЯBЃЌДгЖјХаЖЈЂке§ШЗЃЎ
ЃЈ1ЃЉНсТлЃКABЁЮCDЃЎ
жЄУїЃКЁпACЦНЗжЁЯDABЃЌ
ЁрЁЯ1=ЁЯCABЃЌ
ЁпЁЯ1=ЁЯ2ЃЌ
ЁрЁЯ2=ЁЯCABЃЌ
ЁрABЁЮCDЃЛ
ЃЈ2ЃЉНтЃКШчЭМ2ЃЌ
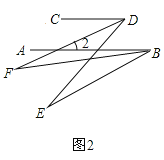
ЁпBFЦНЗжЁЯABEЃЌDFЦНЗжЁЯCDEЃЌ
ЁрЁЯCDFЃН![]() ЁЯCDE=35ЁуЃЌЁЯABE=2ЁЯABFЃЌ
ЁЯCDE=35ЁуЃЌЁЯABE=2ЁЯABFЃЌ
ЁпCDЁЮABЃЌ
ЁрЁЯ2=ЁЯCDF=35ЁуЃЌ
ЁпЁЯ2=ЁЯDFB+ЁЯABFЃЌЁЯDFB=20ЁуЃЌ
ЁрЁЯABF=15ЁуЃЌ
ЁрЁЯABE=2ЁЯABF=30ЁуЃЛ
ЃЈ3ЃЉНтЃКЂкНсТлMGNЕФЖШЪ§ЮЊ15ЁуВЛБфЃЎ
ШчЭМ3ЃЌИљОнШ§НЧаЮЕФЭтНЧаджЪЃЌЁЯ1=ЁЯBPG+ЁЯBЃЌ
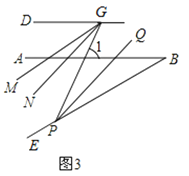
ЁпPQЦНЗжЁЯBPGЃЌGMЦНЗжЁЯDGPЃЌ
ЁрЁЯGPQ=![]() ЁЯBPGЃЌЁЯMGP=
ЁЯBPGЃЌЁЯMGP=![]() ЁЯDGPЃЌ
ЁЯDGPЃЌ
ЁпABЁЮCDЃЌ
ЁрЁЯ1=ЁЯDGPЃЌ
ЁрЁЯMGP=![]() ЃЈЁЯBPG+ЁЯBЃЉЃЌ
ЃЈЁЯBPG+ЁЯBЃЉЃЌ
ЁпPQЁЮGNЃЌ
ЁрЁЯNGP=ЁЯGPQ=![]() ЁЯBPGЃЌ
ЁЯBPGЃЌ
ЁрЁЯMGN=ЁЯMGP-ЁЯNGP=![]() ЃЈЁЯBPG+ЁЯBЃЉ-
ЃЈЁЯBPG+ЁЯBЃЉ-![]() ЁЯBPG=
ЁЯBPG=![]() ЁЯBЃЌ
ЁЯBЃЌ
ИљОнЧАУцЕФЬѕМўЃЌЁЯB=30ЁуЃЌ
ЁрЁЯMGN=![]() ЁС30Ёу=15ЁуЃЌ
ЁС30Ёу=15ЁуЃЌ
ЁрЂйЁЯDGP-ЁЯMGNЕФжЕЫцЁЯDGPЕФБфЛЏЖјБфЛЏЃЛЂкЁЯMGNЕФЖШЪ§ЮЊ15ЁуВЛБфЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжагаRtЁїABCЃЌвбжЊЁЯCAB=90ЁуЃЌAB=ACЃЌAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЕуCЕФзјБъЪЧЃЛ
ЃЈ2ЃЉНЋЁїABCбиxжсе§ЗНЯђЦНвЦЕУЕНЁїAЁфBЁфCЁфЃЌЧвBЃЌCСНЕуЕФЖдгІЕуBЁфЃЌCЁфЧЁКУТфдкЗДБШР§КЏЪ§y= ![]() ЕФЭМЯѓЩЯЃЌЧѓИУЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ЕФЭМЯѓЩЯЃЌЧѓИУЗДБШР§КЏЪ§ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЪ§aЪЙЕУЙигкxЕФВЛЕШЪНзщ ЃЌгаЧвНігаЫФИіећЪ§НтЃЌЧвЪЙЙигкyЕФЗжЪНЗНГЬ
ЃЌгаЧвНігаЫФИіећЪ§НтЃЌЧвЪЙЙигкyЕФЗжЪНЗНГЬ![]() ЃН1гаећЪ§НтЃЌдђЫљгаТњзуЬѕМўЕФећЪ§aЕФжЕжЎКЭЪЧЃЈЁЁЁЁЃЉ
ЃН1гаећЪ§НтЃЌдђЫљгаТњзуЬѕМўЕФећЪ§aЕФжЕжЎКЭЪЧЃЈЁЁЁЁЃЉ
A. 3B. 2C. Љ2D. Љ3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊAЃЈЉ4ЃЌnЃЉЃЌBЃЈ2ЃЌЉ4ЃЉЪЧвЛДЮКЏЪ§yЃНkx+bЕФЭМЯѓКЭЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЕФСНИіНЛЕуЃЎ
ЕФЭМЯѓЕФСНИіНЛЕуЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓжБЯпABгыxжсЕФНЛЕуCЕФзјБъМАЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГівЛДЮКЏЪ§ЕФжЕаЁгкЗДБШР§КЏЪ§жЕЕФxЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊдіЧПбЇЩњЛЗБЃвтЪЖЃЌФГжабЇзщжЏШЋаЃ2000УћбЇЩњВЮМгЛЗБЃжЊЪЖДѓШќЃЌБШШќГЩМЈОљЮЊећЪ§ЃЎДгжаГщШЁВПЗжЭЌбЇЕФГЩМЈНјааЭГМЦЃЌВЂЛцжЦГЩШчЭМЭГМЦЭМЃЎ
ЧыИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЫљГщШЁЕФбљБОШнСПЮЊ ЃЎ
ЃЈ2ЃЉШєГщШЁЕФбЇЩњГЩМЈгУЩШаЮЭМРДУшЪіЃЌдђБэЪОЁАЕкШ§зщЃЈ79.5ЁЋ89.5 ЃЉЁБЕФЩШаЮЕФдВаФНЧЖШЪ§ЮЊЖрЩйЃП
ЃЈ3ЃЉШчЙћГЩМЈдк80ЗжвдЩЯЃЈКЌ80ЗжЃЉЕФЭЌбЇПЩвдЛёНБЃЌЧыЙРМЦИУаЃгаЖрЩйУћЭЌбЇЛёНБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌЙ§ЕуCЕФжБЯпMNЁЮABЃЌDЮЊABБпЩЯ
вЛЕуЃЌЙ§ЕуDзїDEЁЭBCЃЌНЛжБЯпMNгкEЃЌДЙзуЮЊFЃЌСЌНгCDЃЌBEЃЎ
ЃЈ1ЃЉЧѓжЄЃКCE=ADЃЛ
ЃЈ2ЃЉЕБDдкABжаЕуЪБЃЎ
ЂйЧѓжЄЃКЫФБпаЮBECDЪЧСтаЮЃЛ
ЂкЕБЁЯAЮЊЖрЩйЖШЪБЃЌЫФБпаЮBECDЪЧе§ЗНаЮЃПЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМЂйЮЊЦНЕиЩЯвЛДБНЈжўЮягыЬњЫўЭМЃЌЭМЂкЮЊЦфЪОвтЭМЃЎНЈжўЮяABгыЬњЫўCDЖМДЙжБгкЕиУцЃЌBD=20mЃЌдкAЕуВтЕУDЕуЕФИЉНЧЮЊ45ЁуЃЌВтЕУCЕуЕФбіНЧЮЊ58ЁуЃЎЧѓЬњЫўCDЕФИпЖШЃЎЃЈВЮПМЪ§ОнЃКsin58ЁуЁж0.85ЃЌcos58ЁуЁж0.53ЃЌtan58ЁуЁж1.60ЃЉ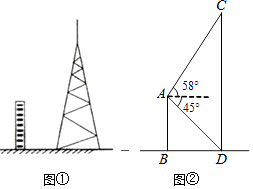
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
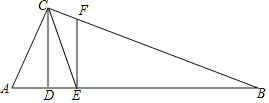
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛИіжБНЧШ§НЧаЮжНЦЌACBЃЌЦфжаЁЯACB=90ЁуЃЌAC=4ЃЌBC=3ЃЌEЃЌFЗжБ№ЪЧACЃЌABБпЩЯЕуЃЌСЌНгEFЃЌНЋжНЦЌACBЕФвЛНЧбиEFелЕўЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌШєелЕўКѓЕуAТфдкABБпЩЯЕФЕуDДІЃЌЧвЪЙSЫФБпаЮECBF=3SЁїAEF ЃЌ дђAE=ЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌШєелЕўКѓЕуAТфдкBCБпЩЯЕФЕуMДІЃЌЧвЪЙMFЁЮCAЃЎЧѓAEЕФГЄЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌШєелЕўКѓЕуAТфдкBCбгГЄЯпЩЯЕФЕуNДІЃЌЧвЪЙNFЁЭABЃЎЧѓAEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гк
гк![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com