
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.

【答案】(1)y=﹣x﹣2;(2)C(﹣2,0),△AOB=6,,(3)﹣4<x<0或x>2.
【解析】
(1)先把B点坐标代入代入y=![]() ,求出m得到反比例函数解析式,再利用反比例函数解析式确定A点坐标,然后利用待定系数法求一次函数解析式;
,求出m得到反比例函数解析式,再利用反比例函数解析式确定A点坐标,然后利用待定系数法求一次函数解析式;
(2)根据x轴上点的坐标特征确定C点坐标,然后根据三角形面积公式和△AOB的面积=S△AOC+S△BOC进行计算;
(3)观察函数图象得到当﹣4<x<0或x>2时,一次函数图象都在反比例函数图象下方.
解:∵B(2,﹣4)在反比例函数y=![]() 的图象上,
的图象上,
∴m=2×(﹣4)=﹣8,
∴反比例函数解析式为:y=﹣![]() ,
,
把A(﹣4,n)代入y=﹣![]() ,
,
得﹣4n=﹣8,解得n=2,
则A点坐标为(﹣4,2).
把A(﹣4,2),B(2,﹣4)分别代入y=kx+b,
得![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为y=﹣x﹣2;
(2)∵y=﹣x﹣2,
∴当﹣x﹣2=0时,x=﹣2,
∴点C的坐标为:(﹣2,0),
△AOB的面积=△AOC的面积+△COB的面积
=![]() ×2×2+
×2×2+![]() ×2×4
×2×4
=6;
(3)由图象可知,当﹣4<x<0或x>2时,一次函数的值小于反比例函数的值.


科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() 与双曲线y=
与双曲线y= ![]() (k>0,x>0)交于点A,将直线y=
(k>0,x>0)交于点A,将直线y= ![]() 向上平移4个单位长度后,与y轴交于点C,与双曲线y=
向上平移4个单位长度后,与y轴交于点C,与双曲线y= ![]() (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A.3
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点的坐标分别是A(3,3),B(1,1),C(4,–1).
(1)直接写出点A、B、C关于x轴对称的点A1、B1、C1的坐标;A1(__________)、B1(__________)、C1(__________).
(2)在图中作出△ABC关于y轴对称的图形△A2B2C2.
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个正整数a可以表示为连续的两个奇数的平方差的形式,如:8=32﹣12,16=52﹣32,24=72﹣52,……,我们则称形如8,16,24这样的正整数a为“奇特数”.
(1)请写出最小的三位“奇特数”,并表示成连续的两个奇数的平方差的形式;
(2)求证:任意一个“奇特数”都是8的倍数;
(3)若一个三位数b为“奇特数”,其百位和个位上的数字相同,十位上的数字比个位上的数字大m(m为正整数),求满足条件的所有三位“奇特数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游商品经销店欲购进A、B两种纪念品,若用380元购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件.
(1)求A、B两种纪念品的进价分别为多少?
(2)若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出时总获利不低于216元,问应该怎样进货,才能使总获利最大,最大为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
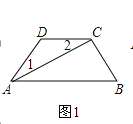
(2)如图,AB∥CD,AB的下方两点E、F满足:BF平分∠ABE、DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度数;
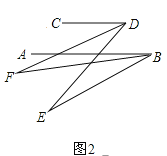
(3)在前面的条件下,若P是BE上一点,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变,可以证明只有一个是正确的,请你作出正确的选择并求值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图1中的BD和CE就是两条三分线.
(1)请你在图2中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(画出一种即可);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,请在图3上画出示意图;
(3)在(2)的前提下,设∠C=x°,试求出x所有可能的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com