
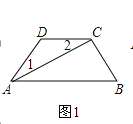
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上
一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D在AB中点时.
①求证:四边形BECD是菱形;
②当∠A为多少度时,四边形BECD是正方形?说明理由.
【答案】
(1)证明:∵DE⊥BC,
∴∠DFB=90°.
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD
(2)①证明:∵D为AB中点,
∴AD=BD.
∵CE=AD,
∴BD=CE.
∵BD∥CE,
∴四边形BECD是平行四边形.
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
②当∠A=45°时,四边形BECD是正方形.
理由如下:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC.
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°.
∵四边形BECD是菱形,∠CDB=90°,
∴四边形BECD是正方形.
【解析】(1)证出AC∥DE,得出四边形ADEC是平行四边形,即可得出结论;
(2)①先证出BD=CE,得出四边形BECD是平行四边形,再由直角三角形斜边上的中线性质得出CD=BD,即可得出四边形BECD是菱形;
②当∠A=45°时,△ABC是等腰直角三角形,由等腰三角形的性质得出CD⊥AB,即可得出四边形BECD是正方形.
【考点精析】利用直角三角形斜边上的中线和平行四边形的判定与性质对题目进行判断即可得到答案,需要熟知直角三角形斜边上的中线等于斜边的一半;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点的坐标分别是A(3,3),B(1,1),C(4,–1).
(1)直接写出点A、B、C关于x轴对称的点A1、B1、C1的坐标;A1(__________)、B1(__________)、C1(__________).
(2)在图中作出△ABC关于y轴对称的图形△A2B2C2.
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游商品经销店欲购进A、B两种纪念品,若用380元购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件.
(1)求A、B两种纪念品的进价分别为多少?
(2)若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出时总获利不低于216元,问应该怎样进货,才能使总获利最大,最大为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
(2)如图,AB∥CD,AB的下方两点E、F满足:BF平分∠ABE、DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度数;
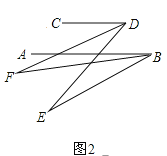
(3)在前面的条件下,若P是BE上一点,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变,可以证明只有一个是正确的,请你作出正确的选择并求值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=3 ![]() ,AC=5,∠B=45°,对于下面四个结论:
,AC=5,∠B=45°,对于下面四个结论:
①∠C一定是钝角; ②△ABC的外接圆半径为3;③sinA= ![]() ;④△ABC外接圆的外切正六边形的边长是
;④△ABC外接圆的外切正六边形的边长是 ![]() .其中正确的个数是( )
.其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,画![]() ,并画
,并画![]() 的平分线
的平分线![]() .
.
(1)将三角尺的直角顶点落在![]() 的任意一点P上,使三角尺的两条直角边与
的任意一点P上,使三角尺的两条直角边与![]() 的两边分别垂直,垂足为E、F(如图1),则
的两边分别垂直,垂足为E、F(如图1),则![]()
![]() (选填<,>,=)
(选填<,>,=)

(2)把三角尺绕着点P旋转(如图2),![]() 与
与![]() 相等吗?试猜想
相等吗?试猜想![]() 、
、![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
拓展延伸1:在(2)条件下,过点P作直线![]() ,分别交
,分别交![]() 、
、![]() 于点G、H,如图3
于点G、H,如图3
①图中全等三角形有多少对(不添加辅助线)
②猜想![]() 、
、![]() 、
、![]() 之间的关系,并证明你的猜想.
之间的关系,并证明你的猜想.
拓展延伸2:
画![]() ,并画
,并画![]() 的平分线
的平分线![]() ,在
,在![]() 上任取一点P,作
上任取一点P,作![]() .
.![]() 的两边分别与
的两边分别与![]() 、
、![]() 相交于E、F两点(如图4),
相交于E、F两点(如图4),![]() 与
与![]() 相等吗?请说明理由.
相等吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com