
ЎѕМвДїЎїИзНјЈ¬»![]() Ј¬Іў»
Ј¬Іў»![]() µДЖЅ·ЦПЯ
µДЖЅ·ЦПЯ![]() Ј®
Ј®
ЈЁ1Ј©Ѕ«ИэЅЗіЯµДЦ±ЅЗ¶ҐµгВдФЪ![]() µДИОТвТ»µгPЙПЈ¬К№ИэЅЗіЯµДБЅМхЦ±ЅЗ±ЯУл
µДИОТвТ»µгPЙПЈ¬К№ИэЅЗіЯµДБЅМхЦ±ЅЗ±ЯУл![]() µДБЅ±Я·Ц±рґ№Ц±Ј¬ґ№ЧгОЄEЎўFЈЁИзНј1Ј©Ј¬Фт
µДБЅ±Я·Ц±рґ№Ц±Ј¬ґ№ЧгОЄEЎўFЈЁИзНј1Ј©Ј¬Фт![]() ЎЎ ЎЎ
ЎЎ ЎЎ![]() ЈЁСЎМоЈјЈ¬ЈѕЈ¬ЈЅЈ©
ЈЁСЎМоЈјЈ¬ЈѕЈ¬ЈЅЈ©

ЈЁ2Ј©°СИэЅЗіЯИЖЧЕµгPРэЧЄЈЁИзНј2Ј©Ј¬![]() Ул
Ул![]() ПаµИВрЈїКФІВПл
ПаµИВрЈїКФІВПл![]() Ўў
Ўў![]() µДґуРЎ№ШПµЈ¬ІўЛµГчАнУЙЈ®
µДґуРЎ№ШПµЈ¬ІўЛµГчАнУЙЈ®
НШХ№СУЙм1ЈєФЪЈЁ2Ј©МхјюПВЈ¬№эµгPЧчЦ±ПЯ![]() Ј¬·Ц±рЅ»
Ј¬·Ц±рЅ»![]() Ўў
Ўў![]() УЪµгGЎўHЈ¬ИзНј3
УЪµгGЎўHЈ¬ИзНј3
ўЩНјЦРИ«µИИэЅЗРОУР¶аЙЩ¶ФЈЁІ»МнјУёЁЦъПЯЈ©
ўЪІВПл![]() Ўў
Ўў![]() Ўў
Ўў![]() Ц®јдµД№ШПµЈ¬ІўЦ¤ГчДгµДІВПлЈ®
Ц®јдµД№ШПµЈ¬ІўЦ¤ГчДгµДІВПлЈ®
НШХ№СУЙм2Јє
»![]() Ј¬Іў»
Ј¬Іў»![]() µДЖЅ·ЦПЯ
µДЖЅ·ЦПЯ![]() Ј¬ФЪ
Ј¬ФЪ![]() ЙПИОИЎТ»µгPЈ¬Чч
ЙПИОИЎТ»µгPЈ¬Чч![]() Ј®
Ј®![]() µДБЅ±Я·Ц±рУл
µДБЅ±Я·Ц±рУл![]() Ўў
Ўў![]() ПаЅ»УЪEЎўFБЅµгЈЁИзНј4Ј©Ј¬
ПаЅ»УЪEЎўFБЅµгЈЁИзНј4Ј©Ј¬![]() Ул
Ул![]() ПаµИВрЈїЗлЛµГчАнУЙЈ®
ПаµИВрЈїЗлЛµГчАнУЙЈ®
Ўѕґр°ёЎїЈЁ1Ј©ЈЅЈ»ЈЁ2Ј©![]() Ј¬АнУЙјыЅвОцЈ»НШХ№СУЙм1ЈєўЩИ«µИИэЅЗРОУР3¶ФЈ»ўЪ
Ј¬АнУЙјыЅвОцЈ»НШХ№СУЙм1ЈєўЩИ«µИИэЅЗРОУР3¶ФЈ»ўЪ![]() Ј¬АнУЙјыЅвОцЈ»НШХ№СУЙм2Јє
Ј¬АнУЙјыЅвОцЈ»НШХ№СУЙм2Јє![]() Ј»АнУЙјыЅвОцЈ»
Ј»АнУЙјыЅвОцЈ»
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭЅЗЖЅ·ЦПЯµДРФЦК¶ЁАнЦ¤ГчЈ»
ЈЁ2Ј©Ц¤ГчЎчMPEЎХЎчNPFЈ¬ёщѕЭИ«µИИэЅЗРОµДРФЦКЦ¤ГчЅбВЫЈ»
НШХ№СУЙм1ЈєўЩёщѕЭµИСьЦ±ЅЗИэЅЗРОµДРФЦКµГµЅOP=PG=PHЈ¬Ц¤ГчЎчGPEЎХЎчOPFЈЁASAЈ©Ј¬ЎчEPOЎХЎчFPHЈ¬ЎчGPOЎХЎчOPHЈ¬µГµЅґр°ёЈ»
ўЪёщѕЭ№ґ№Й¶ЁАнЈ¬И«µИИэЅЗРОµДРФЦКЅвґрЈ»
НШХ№СУЙм2ЈєЧчPGЎНOAУЪGЈ¬PHЎНOBУЪHЈ¬Ц¤ГчЎчPGEЎХЎчPHFЈ¬ёщѕЭИ«µИИэЅЗРОµДРФЦКЦ¤ГчЅбВЫЈ®
ЈЁ1Ј©ЎЯ![]() ЖЅ·Ц
ЖЅ·Ц![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
№Кґр°ёОЄЈєЈЅЈ»
ЈЁ2Ј©![]() Ј¬
Ј¬
АнУЙИзПВЈєЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
УЙЈЁ1Ј©µГЈ¬![]() Ј¬
Ј¬
ФЪ![]() єН
єН![]() ЦРЈ¬
ЦРЈ¬
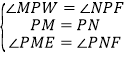 Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј»
Ј»
НШХ№СУЙм1ЈєўЩЎЯ![]() ЖЅ·Ц
ЖЅ·Ц![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯGHЎНOCЈ¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ФЪ![]() єН
єН![]() ЦРЈ¬
ЦРЈ¬
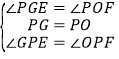 Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Н¬АнЈ¬![]() Ј¬
Ј¬
№Кґр°ёОЄЈє3Ј»
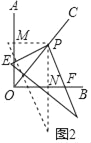
ўЪ![]() Ј¬
Ј¬
АнУЙИзПВЈєЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬
Ўа![]() Ј»
Ј»
НШХ№СУЙм2Јє![]() Ј»
Ј»
АнУЙЈєЧч![]() УЪGЈ¬
УЪGЈ¬![]() УЪHЈ¬
УЪHЈ¬
ЎЯ![]() ЖЅ·Ц
ЖЅ·Ц![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ФЪ![]() єН
єН![]() ЦРЈ¬
ЦРЈ¬
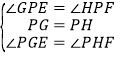 Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
Ўа![]() Ј®
Ј®


 »Ґ¶ЇУўУпПµБРґр°ё
»Ґ¶ЇУўУпПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
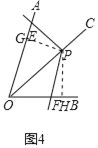
ЎѕМвДїЎїИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПACB=90ЎгЈ¬№эµгCµДЦ±ПЯMNЎОABЈ¬DОЄAB±ЯЙП
Т»µгЈ¬№эµгDЧчDEЎНBCЈ¬Ѕ»Ц±ПЯMNУЪEЈ¬ґ№ЧгОЄFЈ¬Б¬ЅУCDЈ¬BEЈ®
ЈЁ1Ј©ЗуЦ¤ЈєCE=ADЈ»
ЈЁ2Ј©µ±DФЪABЦРµгК±Ј®
ўЩЗуЦ¤ЈєЛД±ЯРОBECDКЗБвРОЈ»
ўЪµ±ЎПAОЄ¶аЙЩ¶ИК±Ј¬ЛД±ЯРОBECDКЗХэ·ЅРОЈїЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
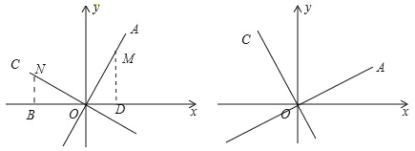
ЎѕМвДїЎїЈЁ1Ј©ОКМвМбіцЈєИзНјТСЦЄЦ±ПЯOAµДЅвОцКЅКЗyЈЅ2xЈ¬OCЎНOAЈ¬ЗуЦ±ПЯOCµДєЇКэЅвОцКЅЈ®
јЧН¬С§МбіцБЛЛыµДПл·ЁЈєФЪЦ±ПЯyЈЅ2xЙПИЎТ»µгMЈ¬№эMЧчxЦбµДґ№ПЯЈ¬ґ№ЧгОЄDЙиµгMµДєбЧш±кОЄmЈ¬ФтµгMµДЧЭЧш±кОЄ2mЈ®јґODЈЅmЈ¬MDЈЅ2mЈ¬И»єуФЪOCЙПЅШИЎONЈЅOMЈ¬№эNЧчxЦбµДґ№ПЯґ№ЧгОЄBЈ®ФтµгNµДЧш±кОЄЎЎ ЎЎЈ¬Ц±ПЯOCµДЅвОцКЅОЄЎЎ ЎЎЈ®
ЈЁ2Ј©НШХ№ЈєТСЦЄЦ±ПЯOAµДЅвОцКЅКЗyЈЅkxЈ¬OCЎНOAЈ¬ЗуЦ±ПЯOCµДєЇКэЅвОцКЅЈ®
ЈЁ3Ј©У¦УГЈєЦ±ЅУРґіцѕ№эPЈЁ2Ј¬3Ј©Ј¬ЗТґ№Ц±УЪЦ±ПЯyЈЅ©Ѓ![]() x+2µДЦ±ПЯЅвОцКЅЎЎ ЎЎЈ®
x+2µДЦ±ПЯЅвОцКЅЎЎ ЎЎЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
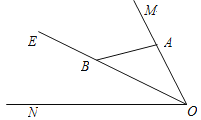
ЎѕМвДїЎїИзНјЈ¬ТСЦЄЎПMONЈЅ80ЎгЈ¬OEЖЅ·ЦЎПMONЈ¬µгAЎўBЎўC·Ц±рКЗЙдПЯOMЎўOEЎўONЙПµД¶Їµг(AЎўBЎўCІ»УлµгOЦШєП)Ј¬Б¬ЅУACЅ»ЙдПЯOEУЪµгDЈ®µ±ABЎНOMЈ¬ЗТЎчADBУРБЅёцПаµИµДЅЗК±Ј¬ЎПOACµД¶ИКэОЄ______________Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
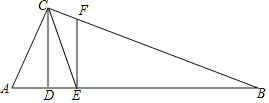
ЎѕМвДїЎїИзНјЈ¬![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() УЪ
УЪ![]() Ј¬
Ј¬![]() ЖЅ·Ц
ЖЅ·Ц![]() Ѕ»
Ѕ»![]() УЪ
УЪ![]() Ј¬
Ј¬![]() Ѕ»
Ѕ»![]() УЪ
УЪ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЦ¤Јє![]() Ј»
Ј»
ЈЁ2Ј©Иф![]() Ј¬Зу
Ј¬Зу![]() µД¶ИКэЈ®
µД¶ИКэЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїјЖЛг
(1)![]() -|
-|![]() -3|
-3|
ЈЁ2Ј©a3![]() 4
4![]() +ЈЁ-a2Ј©3
+ЈЁ-a2Ј©3![]() 2+ЈЁ-2a4Ј©2
2+ЈЁ-2a4Ј©2
ЈЁ3Ј©ЈЁx+2y-3Ј©ЈЁx-2y+3Ј©
ЈЁ4Ј©3(x-2y)2-(2x+y)(-y+2x)-3x(x-0.5y)
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ![]() Ј¬µг
Ј¬µг![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙПЈ¬
ЙПЈ¬![]() Ј¬µг
Ј¬µг![]() ФЪПЯ¶О
ФЪПЯ¶О![]() ЙПЈ¬
ЙПЈ¬![]() Ј¬Б¬ЅУ
Ј¬Б¬ЅУ![]() Ј¬
Ј¬![]() Ј¬Фт
Ј¬Фт![]() µД¶ИКэОЄ______Ј®
µД¶ИКэОЄ______Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
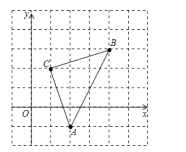
ЎѕМвДїЎїИзНјЈ¬Ц±ЅЗЧш±кПµЦРЈ¬ЎчABCµД¶Ґµг¶јФЪНшёсµгЙПЈ¬ЖдЦРЈ¬CµгЧш±кОЄЈЁ1Ј¬2Ј©Ј¬
ЈЁ1Ј©РґіцµгAЎўBµДЧш±кЈєAЈЁ_____Ј¬_____Ј©ЎўBЈЁ_____Ј¬_____Ј©Ј»
ЈЁ2Ј©Ѕ«ЎчABCПИПтЧуЖЅТЖ2ёцµҐО»і¤¶ИЈ¬ФЩПтЙПЖЅТЖ1ёцµҐО»і¤¶ИЈ¬µГµЅЎчAЎдBЎдCЎдЈ¬РґіцAЎдЎўBЎдЎўCЎдИэµгЧш±кЈ»
ЈЁ3Ј©ЗуЎчABCµДГж»эЎЈ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
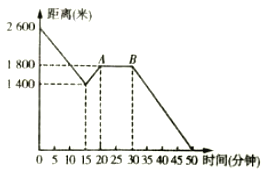
ЎѕМвДїЎїРЗЖЪОеРЎУ±·ЕС§ІЅРРґУѧУ»ШјТЈ¬µ±ЛэЧЯБЛТ»¶ОВ·єуЈ¬ПлЖрТЄИҐВтІК±КЧц»±ЁЈ¬УЪКЗФВ··µ»ШµЅёХѕ№эµДОДѕЯУГЖ·µкЈ¬ВтµЅІК±КєујМРшНщјТЧЯ.ИзНјКЗЛэАлјТµДѕаАлУлЛщУГК±јдµД№ШПµКѕТвНјЈ¬ЗлёщѕЭНјЦРМṩµДРЕПў»ШґрПВБРОКМвЈє
ЈЁ1Ј©РЎУ±јТУлѧУµДѕаАлКЗ ГЧЈ»
ЈЁ2Ј©![]() ±нКѕµДКµјКТвТеКЗ Ј»
±нКѕµДКµјКТвТеКЗ Ј»
ЈЁ3Ј©РЎУ±±ѕґОґУѧУ»ШјТµДХыёц№эіМЦРЈ¬ЧЯµДВ·іМКЗ¶аЙЩГЧЈї
ЈЁ4Ј©ВтµЅІК±КєуЈ¬РЎУ±ґУОДѕЯУГЖ·µк»ШµЅјТІЅРРµДЛЩ¶ИКЗ¶аЙЩГЧ/·ЦЈї
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com