
【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E,F分别是AC,AB边上点,连接EF,将纸片ACB的一角沿EF折叠.
(1)如图①,若折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△AEF , 则AE=;
(2)如图②,若折叠后点A落在BC边上的点M处,且使MF∥CA.求AE的长;
(3)如图③,若折叠后点A落在BC延长线上的点N处,且使NF⊥AB.求AE的长.
【答案】
(1)![]()
(2)解:设AE=x,则CE=4﹣x.
由折叠可知:AE=EM=x,AF=MF,∠AFE=∠MFE,
∵MF∥AC,
∴∠AEF=∠MFE.
∴∠AEF=∠AFE.
∴AE=AF.
∴AE=EM=MF=AF,
∴四边形AEMF为菱形.
∴EM∥AB.∴△CME∽△CBA.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,即AE=
,即AE= ![]()
(3)解:设AE=y,则CE=4﹣y.
由折叠可知:AE=EN=y,AF=NF,
∵NF⊥AB,
∴∠NFB=90°.
∵∠ACB=90°,
∴∠NFB=∠ACB.
且∠NBF=∠ABC,
∴△NBF∽ABC.
∴ ![]() =
= ![]() =
= ![]() .即BF=
.即BF= ![]() NF=
NF= ![]() AF.由BF+AF=AB=5,
AF.由BF+AF=AB=5,
解得:BF= ![]() ,NF=
,NF= ![]() ,
,
∴BN= ![]() =
= ![]() ,
,
∴CN=BN﹣BC= ![]() ﹣3=
﹣3= ![]() .
.
在Rt△CEN中,由勾股定理得:CN2+CE2=EN2,
∴( ![]() )2+(4﹣y)2=y2,
)2+(4﹣y)2=y2,
解得:y= ![]() ,
,
即AE= ![]()
【解析】解:(1)∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF≌S△DEF,
∵S四边形ECBF=3S△EDF,
∴S△ABC=4S△AEF,
在Rt△ABC中,∵∠ACB=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∵∠EAF=∠BAC,
∴△AEF∽△ABC,
∴ ![]() =(
=( ![]() )2,即(
)2,即( ![]() )2=
)2= ![]() ,
,
∴AE= ![]() ;
;
所以答案是: ![]() ;
;
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明;
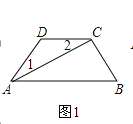
(2)如图,AB∥CD,AB的下方两点E、F满足:BF平分∠ABE、DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度数;
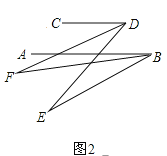
(3)在前面的条件下,若P是BE上一点,G是CD上任一点,PQ平分∠BPG,PQ∥GN,GM平分∠DGP,下列结论:①∠DGP-∠MGN的值不变;②∠MGN的度数不变,可以证明只有一个是正确的,请你作出正确的选择并求值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
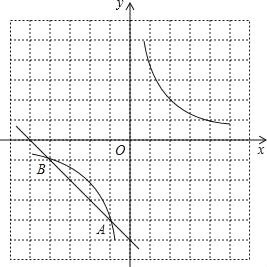
【题目】如图,在方格纸中(小正方形的边长为1),反比例函数的图象与直线的交点A、B均在格点上,根据所给的直角坐标系(O是坐标原点),解答下列问题:
(1)求这个反比例函数的解析式;
(2)若点C在已知的反比例函数的图象上,△ABC是以AB为底的等腰三角形,请写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=3 ![]() ,AC=5,∠B=45°,对于下面四个结论:
,AC=5,∠B=45°,对于下面四个结论:
①∠C一定是钝角; ②△ABC的外接圆半径为3;③sinA= ![]() ;④△ABC外接圆的外切正六边形的边长是
;④△ABC外接圆的外切正六边形的边长是 ![]() .其中正确的个数是( )
.其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,0),B(2,0),点C在y轴上,且S△ABC=3.
(1)求点C的坐标;
(2)以点A、B、C为顶点,作长方形,试写出该长方形第四个顶点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图1中的BD和CE就是两条三分线.
(1)请你在图2中画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(画出一种即可);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,请在图3上画出示意图;
(3)在(2)的前提下,设∠C=x°,试求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①b2>4ac;②4a+b=0;③函数图象与x轴的另一个交点为(2,0);④若点(﹣4,y1)、(﹣1,y2)为函数图象上的两点,则y1<y2 . 其中正确结论是( )
A.②④
B.①④
C.①③
D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com