
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,求
,求 ![]() 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
【答案】
(1)证明:如图,过点O作OF⊥AB于点F,
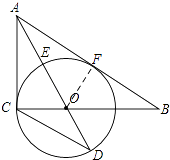
∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
(2)解:如图,连接CE,
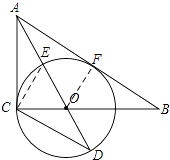
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴ ![]() ,
,
∵tan∠D= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
(3)解:由(2)可知: ![]() =
= ![]() ,
,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴ ![]() ,
,
∴AC2=AEAD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
由(1)可知:AC=AF=4,
∠OFB=∠ACB=90°,
∵∠B=∠B,
∴△OFB∽△ACB,
∴ ![]() =
= ![]() ,
,
设BF=a,
∴BC= ![]() ,
,
∴BO=BC﹣OC= ![]() ﹣3,
﹣3,
在Rt△BOF中,
BO2=OF2+BF2,
∴( ![]() ﹣3)2=32+a2,
﹣3)2=32+a2,
∴解得:a= ![]() 或a=0(不合题意,舍去),
或a=0(不合题意,舍去),
∴AB=AF+BF= ![]() .
.
【解析】(1)证AB是⊙O的切线,需要证明AB垂直半径,为此过点O作OF⊥AB于点F,再证明OF是半径可得证;
(2)连接CE,先证明△ACE∽△ADC,从而利用相似三角形的对应边成比例得到![]() ,再由tan∠D的值可求得答案;
,再由tan∠D的值可求得答案;
(3)由△ACE∽△ADC,再利用相似三角形的对应边成比例得到AE、AC的长,设BF=a,再证明△OFB∽△ACB,利用相似三角形的对应边成比例可用a表示出BO,在Rt△BOF中,由勾股定理可求出a的值,进而求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填空:
(a-b)(a+b)=________;
(a-b)(a2+ab+b2)=________;
(a-b)(a3+a2b+ab2+b3)=________;
(2)猜想:
(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1)=________(其中n为正整数,且n≥2);
(3)利用(2)猜想的结论计算:
①29+28+27+…+22+2+1;
②210-29+28-…-23+22-2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中∠BAC=135°,点E,点F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,BE=12,CF=9.
(1)判断△EAF的形状,并说明理由;
(2)求△EAF的周长.
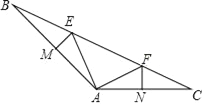
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
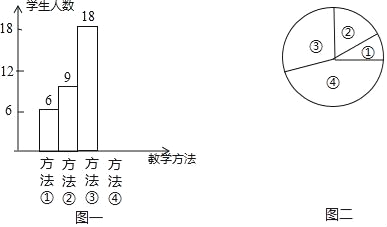
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,作者是我国明代数学家程大位.在《算法统宗》中记载:“以绳测井,若将绳三折测之,绳多4尺,若将绳四折测之,绳多1尺,绳长井深各几何?”
译文:“用绳子测水井深度,如果将绳子折成三等份,井外余绳4尺;如果将绳子折成四等份,井外余绳1尺.问绳长、井深各是多少尺?”
设井深为x尺,根据题意列方程,正确的是( )

A. 3(x+4)=4(x+1) B. 3x+4=4x+1
C. 3(x﹣4)=4(x﹣1) D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
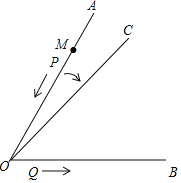
【题目】如图,已知∠AOB=60°,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO、射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为lcm/s;P、Q同时出发,同时射线OC绕着点O从OA上以每秒5°的速度顺时针旋转,设运动时间是t(s).
(1)当点P在MO上运动时,PO=______cm(用含t的代数式表示);
(2)当点P在线段MO上运动时,t为何值时,OP=OQ?此时射线OC是∠AOB的角平分线吗?如果是请说明理由.
(3)在射线OB上是否存在P、Q相距2cm?若存在,请求出t的值并求出此时∠BOC的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
专业知识 | 74 | 87 | 90 |
语言能力 | 58 | 74 | 70 |
综合素质 | 87 | 43 | 50 |
(1)如果根据三次测试的平均成绩确定人选,那么谁将被录用?
(2)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(3)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com