
【题目】“小组合作制”正在七年级如火如茶地开展,旨在培养七年级学生的合作学习的精神和能力,学会在合作中自主探索.数学课上,吴老师在讲授“角平分线”时,设计了如下四种教学方法:①教师讲授,学生练习;②学生合作交流,探索规律;③教师引导学生总结规律,学生练习;④教师引导学生总结规律,学生合作交流,吴老师将上述教学方法作为调研内容发到七年级所有同学手中要求每位同学选出自己最喜欢的一种,然后吴老师从所有调查问卷中随机抽取了若干份调查问卷作为样本,统计如下:
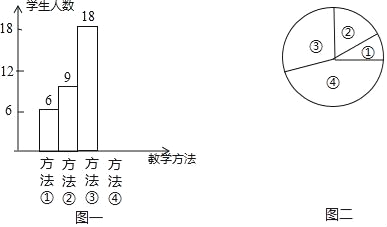
序号①②③④代表上述四种教学方法,图二中,表示①部分的扇形的中心角度数为36°,请回答问题:
(1)在后来的抽样调查中,吴老师共抽取 位学生进行调查;并将条形统计图补充完整;
(2)图二中,表示③部分的扇形的中心角为多少度?
(3)若七年级学生中选择④种教学方法的有540人,请估计七年级总人数约为多少人?
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于O,OE⊥AB,OF⊥CD.
(1)图中与∠AOF互余的角是______,与∠COE互补的角是______;(把符合条件的角都写出来)
(2)如果∠AOC=![]() ∠EOF,求∠EOF的度数.
∠EOF,求∠EOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1和l2于B、C两点,连接AC、BC,若∠ABC=65°,则∠1的度数是( )

A. 35° B. 50° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△PQR在直角坐标系中的位置如图所示:
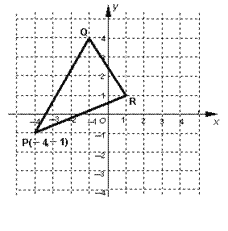
(1) 求出△PQR的面积;
(2) 画出△P′Q′R′,使△P′Q′R′与△PQR关于y轴对称,写出点P′、Q′、R′的坐标;
(3)连接PP′,QQ′,判断四边形QQ′P′P的形状,求出四边形QQ′P′P的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD= ![]() ,求
,求 ![]() 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.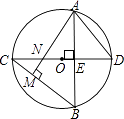
(1)求证:AD=AN;
(2)若AB=4 ![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:
如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°.判断DB与DC的大小关系并证明.
探究:
如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,DB与DC的大小关系变吗?请说明理由.
应用:
如图③,四边形ABDC中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= .(用含a的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com