
【题目】如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、
BF,点M是BF上一点且![]() =
=![]() ,过点M作MN⊥BC于点N,连接FN,则
,过点M作MN⊥BC于点N,连接FN,则![]() = .
= .

【答案】![]()
【解析】
试题分析:根据正方形的性质得到∠A=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA,AD∥BC.设AE=a,则DE=a,AB=BC=CD=DA=2a.根据勾股定理得到BE=![]() a,CE=
a,CE=![]() a,得到BE=CE,过点F作FG⊥AD于G,FG交BC于H.根据FG∥CD,点F是CE的中点,得到EG=DG=
a,得到BE=CE,过点F作FG⊥AD于G,FG交BC于H.根据FG∥CD,点F是CE的中点,得到EG=DG=![]() DE=
DE=![]() a,GF=
a,GF=![]() CD=a.根据三角函数的定义得到∠AEB=∠GDF,由平行线的性质得到∠BEF=∠DFE,推出△EFG≌△CFH,根据全等三角形的性质得到FG=FH=a,EG=CH=
CD=a.根据三角函数的定义得到∠AEB=∠GDF,由平行线的性质得到∠BEF=∠DFE,推出△EFG≌△CFH,根据全等三角形的性质得到FG=FH=a,EG=CH=![]() a.推出四边形CDGH是矩形,根据矩形的性质得到CH=DG=
a.推出四边形CDGH是矩形,根据矩形的性质得到CH=DG=![]() a,根据平行线分线段成比例定理得到
a,根据平行线分线段成比例定理得到![]() =
=![]() =
=![]() ,于是得到MN=
,于是得到MN=![]() FH=
FH=![]() a,BN=
a,BN=![]() BH=
BH=![]() a,求得S△FMN=
a,求得S△FMN=![]() =
=![]()
![]() a×a=
a×a=![]() a2,S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣
a2,S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣![]() 2aa﹣
2aa﹣![]() ﹣
﹣![]() =
=![]() a2.即可得到结论.
a2.即可得到结论.
解:∵四边形ABCD是正方形,
∴∠A=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA,AD∥BC.
设AE=a,则DE=a,AB=BC=CD=DA=2a.
在△ABE中,由勾股定理,得BE=![]() a,
a,
在△CDE中,由勾股定理,得CE=![]() a,
a,
∴BE=CE,
过点F作FG⊥AD于G,FG交BC于H.
∵AD∥BC,FG⊥AD,∴GH⊥BC.
∵FG∥CD,点F是CE的中点,
∴EG=DG=![]() DE=
DE=![]() a,GF=
a,GF=![]() CD=a.
CD=a.
在直角△ABE中,∵tan∠AEB=![]() =
=![]() =2,
=2,
在直角△GFD中,∵tan∠GDF=![]() =
=![]() =2,
=2,
∴tan∠AEB=tan∠GDF,
∵0°<∠AEB<90°,0°<∠GDF<90°,
∴∠AEB=∠GDF,
∴BE∥DF,
∴∠BEF=∠DFE,
在△EFG与△CFH中, ,
,
∴△EFG≌△CFH,
∴FG=FH=a,EG=CH=![]() a.
a.
∵GH∥CD,GD∥HC,∠CDA=90°,
∴四边形CDGH是矩形,
∴CH=DG=![]() a,
a,
∴BH=BC﹣CH=![]() a.
a.
∵MN⊥BC,GH⊥BC,
∴MN∥FH,
∴![]() =
=![]() =
=![]() ,
,
∴MN=![]() FH=
FH=![]() a,BN=
a,BN=![]() BH=
BH=![]() a,
a,
∴MN=![]() AB,
AB,
∵BN=CH=![]() a,
a,
∴NH=BC﹣BN﹣CH=a,
∴S△FMN=![]() =
=![]()
![]() a×a=
a×a=![]() a2,
a2,
S四边形FEBN=S正方形ABCD﹣S△ABE﹣S△CDE﹣S△CNF=4a2﹣![]() 2aa﹣
2aa﹣![]() ﹣
﹣![]() =
=![]() a2.
a2.
∴![]() =
=![]()
![]() =
=![]() .
.
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,已知第二象限的点A在反比例函数y=![]() 上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=
上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=![]() 上,则k的值为( )
上,则k的值为( )

A.﹣2![]() B.﹣
B.﹣![]() C.2
C.2![]() D.﹣4
D.﹣4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
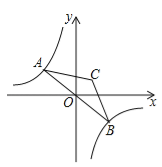
【题目】如图,点A是双曲线![]() 在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线
在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线![]() 上运动,则k的值为( )
上运动,则k的值为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com