
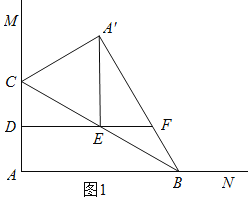
【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.

【答案】![]() 或4
或4
【解析】当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图1,根据对称的性质和平行线可得:A'C=A'E=4,根据直角三角形斜边中线的性质得:BC=2A'B=8,最后利用勾股定理可得AB的长;
②当∠A'FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.
当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图1,
 .
.
∵△A′BC与△ABC关于BC所在直线对称,
∴A'C=AC=4,∠ACB=∠A'CB,
∵点D,E分别为AC,BC的中点,
∴D、E是△ABC的中位线,
∴DE∥AB,
∴∠CDE=∠MAN=90°,
∴∠CDE=∠A'EF,
∴AC∥A'E,
∴∠ACB=∠A'EC,
∴∠A'CB=∠A'EC,
∴A'C=A'E=4,
Rt△A'CB中,∵E是斜边BC的中点,
∴BC=2A'E=8,
由勾股定理得:AB2=BC2-AC2,
∴AB=![]() ;
;
②当∠A'FE=90°时,如图2,
 .
.
∵∠ADF=∠A=∠DFB=90°,
∴∠ABF=90°,
∵△A′BC与△ABC关于BC所在直线对称,
∴∠ABC=∠CBA'=45°,
∴△ABC是等腰直角三角形,
∴AB=AC=4;.
综上所述,AB的长为4![]() 或4;
或4;
故答案为:4![]() 或4.
或4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 边长为
边长为![]() 的等边三角形
的等边三角形![]() 的顶点
的顶点![]() 分别在边
分别在边![]() ,
,![]() 上当
上当![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在边
随之在边![]() 上运动,等边三角形的形状保持不变,运动过程中,点
上运动,等边三角形的形状保持不变,运动过程中,点![]() 到点
到点![]() 的最大距离为( )
的最大距离为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰勒斯是古希腊哲学家,相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图,B是观察点,船A在B的正前方,过B作AB的垂线,在垂线上截取任意长BD,C是BD的中点,观察者从点D沿垂直于BD的DE方向走,直到点E、船A和点C在一条直线上,那么△ABC≌△EDC,从而量出DE的距离即为船离岸的距离AB,这里判定△ABC≌△EDC的方法是( )

A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应的任务:求根分解法是多项式因式分解的一种方法,是用求多项式对应的方程的根分离出多项式的一次因式.
设f(x)是一元多项式,若方程f(x)=0有一个根为x=a,则多项式必有一个一次因式x﹣a,于是f(x)=(x﹣a)g(x).
例如,设多项式7x2﹣x﹣6为f(x),则有f(x)=7x2﹣x﹣6,令7x2﹣x﹣6=0,容易看出,此方程有一根为x=1,则f(x)必有一个一次因式x﹣1,那么得到7x2﹣x﹣6=(x﹣1)(mx+n)(m、n为常数)而(x﹣1)(mx+n)=mx2+(n﹣m)x﹣n,所以7x2﹣x﹣6=mx2+(n﹣m)x﹣n,由系数对应相等可得m=7,n=6,所以7x2﹣x﹣6=(x﹣1)(7x+6).
任务:(1)方程x3﹣3x2+4=0的一根为 .
(2)请你根据上面的材料因式分解多项式:x3﹣3x2+4= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明利用所学函数知识,对函数![]() 进行了如下研究.列表如下:
进行了如下研究.列表如下:
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | 7 | 5 | 3 | m | 1 | n | 1 | 1 | 1 | … |

(1)自变量x的取值范围是________;
(2)表格中:m=_______;n=________;
(3)在给出的坐标系中画出函数![]() 的图象;
的图象;
(4)一次函数![]() 的图象与函数
的图象与函数![]() 的图象交点的坐标为_______________.
的图象交点的坐标为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若AB=3,BC=4,求四边形OCED的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,点F、E分别在边AC、AB上,连接DE、DF,且∠AFD+∠B=180°.
(1)求证:BD=FD;
(2)当AF+FD=AE时,求证:∠AFD=2∠AED.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com