
����Ŀ����ͼ��ʾ����֪��ABC�У�AB=AC=BC=10���ף�M��N�ֱ�ӵ�A����Bͬʱ�������������εı��˶�����֪��M���ٶ���1����/����ٶȣ���N���ٶ���2����/�룬����N��һ�ε���B��ʱ��M��Nͬʱֹͣ�˶���
��1��M��Nͬʱ�˶������M��N�����غϣ�
��2��M��Nͬʱ�˶�����ɵõȱ���������AMN��
��3��M��N��BC�����˶�ʱ���ܷ�õ���MNΪ�ױߵĵ�����AMN��������ڣ��������ʱM��N�˶���ʱ�䣿

���𰸡�(1)10��;(2)![]() ��;(3)
��;(3)![]() ��.
��.
��������
��1���������M��N�˶�x���M��N�����غϣ���ʾ��M��N���˶�·�̣�N���˶�·�̱�M���˶�·�̶�10cm���г�������⼴�ɣ�
��2�������������M��N�˶�t��ɵõ��ȱ������Ρ�AMN��Ȼ���ʾ��AM��AN�ij������ڡ�A����60��������ֻҪAM=AN������ANM���ǵȱ������Σ�
��3�����ȼ����AMN�ǵ��������Σ���֤����ACM�ա�ABN���ɵ�CM=BN������˶�ʱ�䣬��ʾ��CM��NB�ij����г����̣��ɽ��δ֪����
��1�����M��N�˶�x���M��N�����غϣ�
x+10=2x�����x=10��
��2�����M��N�˶�t��ɵõ��ȱ���������AMN����ͼ����
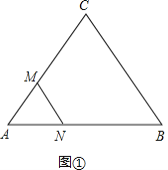
AM=t��AN=AB�CBN=10�C2t��
����������AMN�ǵȱ������Σ�
��t=10�C2t�����t=![]() ��
��
����M��N�˶�![]() ��ɵõ��ȱ���������AMN��
��ɵõ��ȱ���������AMN��
��3������M��N��BC�����˶�ʱ�����Եõ���MNΪ�ױߵĵ��������Σ�
�ɣ�1��֪10��ʱM��N�����غϣ�ǡ���ڵ�C����
��ͼ����������AMN�ǵ��������Σ�
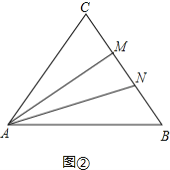
��AN=AM�����AMN=��ANM�����AMC=��ANB��
��AB=BC=AC�����ACB�ǵȱ������Σ����C=��B��
����ACM����ABN��
�� ��
��
���ACM�ա�ABN��AAS����
��CM=BN��
�赱��M��N��BC�����˶�ʱ��M��N�˶���ʱ��Ϊy��ʱ����AMN�ǵ��������Σ�
��CM=y�C10��NB=30�C2y��CM=NB��
y�C10=30�C2y��
��ã�y=![]() ���ʼ��������
���ʼ��������
������M��N��BC�����˶�ʱ���ܵõ���MNΪ�ױߵĵ�����AMN����ʱM��N�˶���ʱ��Ϊ![]() �룮
�룮


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��������ǣ�
��������ǣ�![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��

![]() ��֤���ı���
��֤���ı���![]() �����Σ�
������
![]() ��
��![]() ������
������![]() ����
����![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MAN=90������C�ڱ�AM�ϣ�AC=4����BΪ��AN��һ���㣬����BC����A��BC����ABC����BC����ֱ�߶Գƣ���D��E�ֱ�ΪAC��BC���е㣬����DE���ӳ���A��B����ֱ���ڵ�F������A��E������A��EFΪֱ��������ʱ��AB�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
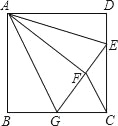
����Ŀ����ͼ��������ABCD�У�AB=6����E�ڱ�CD�ϣ���CD=3DE������ADE��AE��������AFE���ӳ�EF����BC�ڵ�G������AG��CF�����н��ۣ��١�ABG�ա�AFG����BG=GC����AG��CF����S��FGC=3��������ȷ���۵���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=30�㣬BC=2����D�DZ�AB�ϵĶ��㣬����ACD��CD���ڵ�ֱ���۵�����CDA��λ�ã�CA'��AB�ڵ�E������A'EDΪֱ�������Σ���AD�ij�Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,![]() ��,
��,![]() ��
��![]() ��ֱ
��ֱ![]() �Ľ�ƽ������
�Ľ�ƽ������![]() ,
,![]() Ϊ
Ϊ![]() ���е�,��ͼ��������Ӱ�������֮������ֵΪ( )
���е�,��ͼ��������Ӱ�������֮������ֵΪ( )
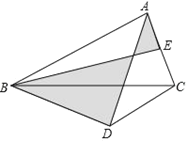
A.1.5B.3C.4.5D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У�ÿ��С�����εı߳�Ϊ1����λ���ȣ���֪��ABC�Ķ���A��C������ֱ�Ϊ����4��4��������1��2������B����Ϊ����2��1����
��1������ͼ����ȷ������ƽ��ֱ������ϵ��������B��������AB��BC��
��2������ABC��x��������ƽ��5����λ���Ⱥ�����x�ᷭ�۵õ���DEF��������DEF��
��3����P��m��n������ABC�ı��ϵ�һ�㣬������2���еı仯��õ���Ӧ��Q��ֱ��д����Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����εı߳���Ϊ1�ķ���ֽ�У��߶�AB�Ķ˵�A��B����С�����εĶ����ϣ�
��1���ڷ���ֽ�л�����ABΪһ��ֱ�DZߵĵ���ֱ����ABC������C��С�����εĶ����ϣ�
��2���ڷ���ֽ�л�����ABC������BD�����߶�DC�Ƶ�C˳ʱ����ת90���õ��߶�CD����������ת����߶�CD��������BD����ֱ��д���ı���BDCD���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��ƽ���߽��ڵ�
��ƽ���߽��ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() �ܳ��ֱ�Ϊ
�ܳ��ֱ�Ϊ![]() ��
��![]() .
.

(1)��֤��![]() ��
��
(2)�߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com