
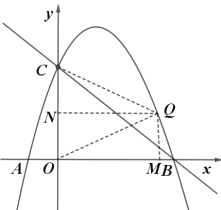
【题目】如图,抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
x+c经过点A(﹣1,0)和点C (0,3)与x轴的另一交点为点B,点M是直线BC上一动点,过点M作MP∥y轴,交抛物线于点P.
(1)求该抛物线的解析式;
(2)在抛物线上是否存在一点Q,使得△QCO是等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)以M为圆心,MP为半径作⊙M,当⊙M与坐标轴相切时,求出⊙M的半径.

【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)不存在,理由见解析;(3)⊙M的半径为
x+3;(2)不存在,理由见解析;(3)⊙M的半径为![]() 或
或![]()
【解析】
(1)已知抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C(0,3),利用待定系数法即可求得抛物线解析式;
x+c经过点A(﹣1,0)和点C(0,3),利用待定系数法即可求得抛物线解析式;
(2)在抛物线上找到一点Q,使得△QCO是等边三角形,过点Q作OM⊥OB于点M,过点Q作QN⊥OC于点N,根据△QCO是等边三角形,求得Q点坐标,再验证Q点是否在抛物线上;
(3)分两种情况①当⊙M与y轴相切,如图所示,令M点横坐标为t,PM=t,将PM用t表示出来,列出关于t的一元二次方程,求得t,进而求得半径;②⊙M与x轴相切,过点M作MN⊥OB于N,如图所示,令M点横坐标为m,因为PN=2MN,列出关于m的一元二次方程,即可求出m,进而求得⊙M的半径.
(1)∵抛物线y=ax2+![]() x+c经过点A(﹣1,0)和点C(0,3)
x+c经过点A(﹣1,0)和点C(0,3)
∴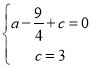
解得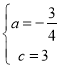
∴该抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+3
x+3
故答案为:y=﹣![]() x2+
x2+![]() x+3
x+3
(2)在抛物线上找到一点Q,使得△QCO是等边三角形,过点Q作OM⊥OB于点M,过点Q作QN⊥OC于点N
∵△QCO是等边三角形,OC=3
∴CN=![]()
∴NQ=![]()
即Q(![]() ,
,![]() )
)
当x=![]() 时,y=﹣
时,y=﹣![]() ×(
×(![]() )2+
)2+![]() ×
×![]() +3=
+3=![]() ≠
≠![]()
∴Q(![]() ,
,![]() )不在抛物线上
)不在抛物线上
y=﹣![]() x2+
x2+![]() x+3
x+3
故答案为:不存在,理由见解析
(3)①⊙M与y轴相切,如图所示
∵y=﹣![]() x2+
x2+![]() x+3
x+3
当y=0时,﹣![]() x2+
x2+![]() x+3=0
x+3=0
解得x1=-1,x2=4
∴B(4,0)
令直线BC的解析式为y=kx+b
![]()
解得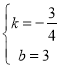
∴直线BC的解析式为![]()
令M点横坐标为t
∵MP∥y轴,⊙M与y轴相切
∴t=﹣![]() t2+
t2+![]() t+3-
t+3-![]()
解得t=![]()
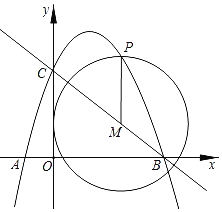
⊙M的半径为![]()
②⊙M与x轴相切,过点M作MN⊥OB于N,如图所示
令M点横坐标为m
∵PN=2MN
∴![]()
解得m=1或m=4(舍去)
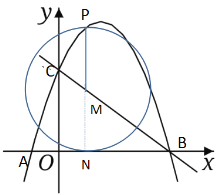
∴⊙M的半径为:
![]()
故答案为:⊙M的半径为![]() 或
或![]()


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
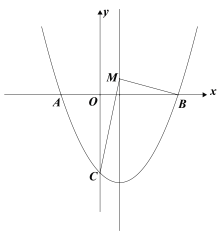
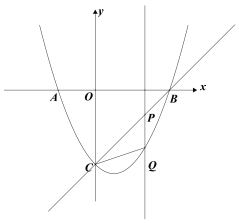
【题目】如图,抛物线y=![]() x2+mx+4m与x轴交于点A(
x2+mx+4m与x轴交于点A(![]() ,0)和点B(
,0)和点B(![]() ,0),与y轴交于点C,
,0),与y轴交于点C,![]() ,若对称轴在y轴的右侧.
,若对称轴在y轴的右侧.
(1)求抛物线的解析式
(2)在抛物线的对称轴上取一点M,使|MC-MB|的值最大;
(3)点Q是抛物线上任意一点,过点Q作PQ⊥x轴交直线BC于点P,连接CQ,当△CPQ是等腰三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
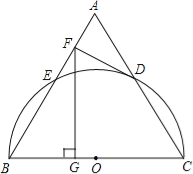
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )
A.众数是36.5B.中位数是36.7
C.平均数是36.6D.方差是0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
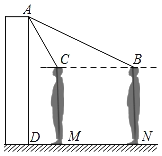
【题目】某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门AD的顶部A处距地面高为2.2m,为了解自己的有效测温区间.身高1.6m的小聪做了如下实验:当他在地面N处时测温门开始显示额头温度,此时在额头B处测得A的仰角为18°;在地面M处时,测温门停止显示额头温度,此时在额头C处测得A的仰角为60°.求小聪在地面的有效测温区间MN的长度.(额头到地面的距离以身高计,计算精确到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
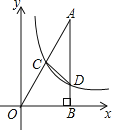
【题目】如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=![]() (x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2,当a≤x≤b时m≤y≤n,则下列说法正确的是( )
A.当n﹣m=1时,b﹣a有最小值
B.当n﹣m=1时,b﹣a有最大值
C.当b﹣a=1时,n﹣m无最小值
D.当b﹣a=1时,n﹣m有最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
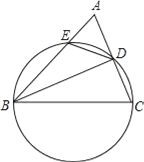
【题目】如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是( )
A. BD⊥AC B. AC2=2ABAE C. △ADE是等腰三角形 D. BC=2AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡市灵山胜境公司厂生产一种新的大佛纪念品,每件纪念品制造成本为18元,试销过程发现,每月销量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间的关系可以近似地看作一次函数
之间的关系可以近似地看作一次函数![]() .
.
![]() 写出公司每月的利润
写出公司每月的利润![]() 万元
万元![]() 与销售单价
与销售单价![]() 元
元![]() 之间函数解析式;
之间函数解析式;
![]() 当销售单价为多少元时,公司每月能够获得最大利润?最大利润是多少?
当销售单价为多少元时,公司每月能够获得最大利润?最大利润是多少?
![]() 根据工商部门规定,这种纪念品的销售单价不得高于32元
根据工商部门规定,这种纪念品的销售单价不得高于32元![]() 如果公司要获得每月不低于350万元的利润,那么制造这种纪念品每月的最低制造成本需要多少万元?
如果公司要获得每月不低于350万元的利润,那么制造这种纪念品每月的最低制造成本需要多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com