
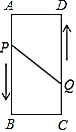
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以2厘米/秒的速度向终点
以2厘米/秒的速度向终点![]() 移动,点
移动,点![]() 以1厘米/秒的速度向
以1厘米/秒的速度向![]() 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为
移动,当有一点到达终点时,另一点也停止运动.设运动的时间为![]() 秒,当
秒,当![]() ________时,以点
________时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.
【答案】![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
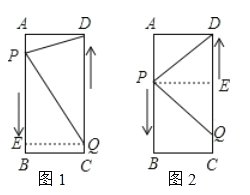
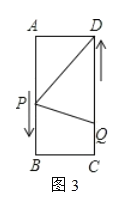
分情况讨论,如图1,当PQ=DQ时,如图2,当PD=PQ时,如图3,当PD=QD时,由等腰三角形的性质及勾股定理建立方程就可以得出结论.
解:如图1,当PQ=DQ时,作QE⊥AB于E,
∴∠PEQ=90°,
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴QE=BC=2cm,BE=CQ=t.
∵AP=2t,
∴PE=6﹣2t﹣t=6﹣3t.DQ=6﹣t.
∵PQ=DQ,
∴PQ=6﹣t.
在Rt![]() PQE中,由勾股定理,得
PQE中,由勾股定理,得
(6﹣3t)2+4=(6﹣t)2,
解得:t=![]() .
.
如图2,当PD=PQ时,
作PE⊥DQ于E,
∴DE=QE=![]() DQ,∠PED=90°.
DQ,∠PED=90°.
∵∠B=∠C=90°,
∴四边形BCQE是矩形,
∴PE=BC=2cm.
∵DQ=6﹣t,
∴DE=![]() .
.
∴2t=![]() ,
,
解得:t=![]() ;
;
如图5,当PD=QD时,
∵AP=2t,CQ=t,
∴DQ=6﹣t,
∴PD=6﹣t.
在Rt![]() APD中,由勾股定理,得
APD中,由勾股定理,得
4+4t2=(6﹣t)2,
解得t1=![]() ,t2=
,t2=![]() (舍去).
(舍去).
综上所述:t=![]() ,
,![]() ,
,![]() ,
,![]() .
.
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】(12分)如图,平面直角坐标系![]() 中点
中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点,连接
三点,连接![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() .
.
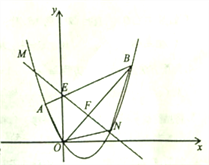
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的函数解析式;
(3)点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 轴右侧),连接
轴右侧),连接![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标并求出四边形
的坐标并求出四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的等边三角形ABC中,D是AB边上的一动点,由A向B运动(A、B不重合),F是BC延长线上的一动点,与D同时以相同的速度由C向BC延长线方向运动(与C不重合),过点D作DE⊥AC,连接DF交AC于G.
(1)当点D运动到AB的中点时,直接写出AE的长.
(2)当DF⊥AB时,求AD的长.
(3)在运动过程中线段GE的长是否发生变化?如果不变,求出线段GE的长:如果发生改变请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作![]() ,与AC、DC分别交于点
,与AC、DC分别交于点![]() 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、![]() 下列结论:
下列结论: ![]() ;
; ![]() ≌
≌![]() ;
; ![]() ;
; ![]() 若
若![]() ,则
,则![]() 其中结论正确的有
其中结论正确的有![]()
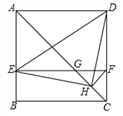
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
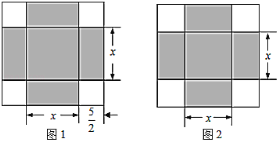
【题目】《代数学》中记载,形如![]() 的方程,求正数解的几何方法是:“如图1,先构造一个面积为
的方程,求正数解的几何方法是:“如图1,先构造一个面积为![]() 的正方形,再以正方形的边长为一边向外构造四个面积为
的正方形,再以正方形的边长为一边向外构造四个面积为![]() 的矩形,得到大正方形的面积为
的矩形,得到大正方形的面积为![]() ,则该方程的正数解为
,则该方程的正数解为![]() .”小聪按此方法解关于
.”小聪按此方法解关于![]() 的方程
的方程![]() 时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
A.6B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据如表回答下列问题:
x | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
x2 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
(1)275.56的平方根是______ ;
(2)![]() = ______ ;
= ______ ;
(3)查看上表, <![]() < .
< .
查看答案和解析>>
科目:初中数学 来源: 题型:
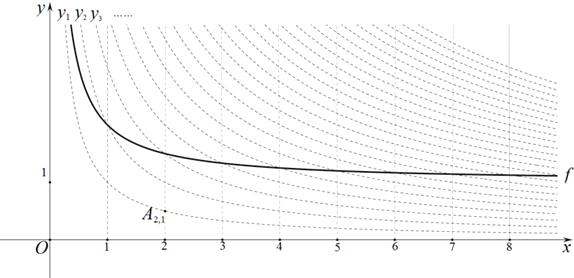
【题目】如图,在平面直角坐标系xOy中,定义直线![]() 与双曲线
与双曲线![]() 的交点
的交点![]() 、n为正整数
、n为正整数![]() 为“双曲格点”,双曲线
为“双曲格点”,双曲线![]() 在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
在第一象限内的部分沿着竖直方向平移或以平行于x轴的直线为对称轴进行翻折之后得到的函数图象为其“派生曲线”.
![]() “双曲格点”
“双曲格点”![]() 的坐标为______;
的坐标为______; ![]() 若线段
若线段![]() 的长为1个单位长度,则
的长为1个单位长度,则![]() ______;
______;
![]() 图中的曲线f是双曲线
图中的曲线f是双曲线![]() 的一条“派生曲线”,且经过点
的一条“派生曲线”,且经过点![]() ,则f的解析式为
,则f的解析式为![]() ______;
______;
![]() 画出双曲线
画出双曲线![]() 的“派生曲线”
的“派生曲线”![]() 与双曲线
与双曲线![]() 不重合
不重合![]() ,使其经过“双曲格点”
,使其经过“双曲格点”![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,一条生产线的流水线上依次有5个机器人,它们站立的位置在数轴上依次用点A1,A2,A3,A4,A5表示.

(1)若原点是零件的供应点,5个机器人分别到供应点取货的总路程是多少?
(2)若将零件的供应点改在A1,A3,A5中的其中一处,并使得5个机器人分别到达供应点取货的总路程最短,你认为应该在哪个点上?通过计算说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com