
【题目】(12分)如图,平面直角坐标系![]() 中点
中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点,连接
三点,连接![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() .
.
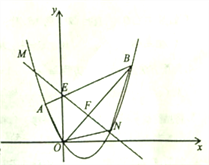
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的函数解析式;
(3)点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 轴右侧),连接
轴右侧),连接![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标并求出四边形
的坐标并求出四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3) 最大值为
;(3) 最大值为![]() ,此时
,此时![]() 点坐标为
点坐标为![]()
【解析】试题分析:(1)先利用待定系数法求出直线![]() 的解析式,然后计算自变量为0时的函数值即可得到
的解析式,然后计算自变量为0时的函数值即可得到![]() 点坐标;
点坐标;
(2)利用待定系数求抛物线的解析式;
(3)如图1,作![]() 轴交
轴交![]() 于 G,如图,利用一次函数和二次函数图象上点的坐标特征,设设
于 G,如图,利用一次函数和二次函数图象上点的坐标特征,设设![]() ,则
,则![]() ,再根据三角形面积公式计算出
,再根据三角形面积公式计算出
![]() 和
和![]() 然后得到S四边形ABNO和m的二次函数关系式,再根据二次函数的性质求解;
然后得到S四边形ABNO和m的二次函数关系式,再根据二次函数的性质求解;
试题解析:(1)设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,解得
,解得 ,
,
所以直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() 点坐标为
点坐标为![]() ;
;
(2)设抛物线解析式为![]() ,
,
把![]() 代入得
代入得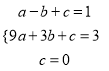 ,解得
,解得 ,
,
所以抛物线解析式为![]() ;
;
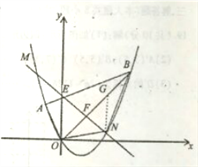
(3)如图1,作![]() 轴交
轴交![]() 的解析式为
的解析式为![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]()
所以![]()
当![]() 时,四边形
时,四边形![]() 面积的最大值,最大值为
面积的最大值,最大值为![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;
;


科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结 合.研究数轴我们发现了许多重要的规律:若数轴上点 A、点 B 表示的数分别为 a、b,则A、B 两点之间的距离 AB= ![]() ,线段 AB 的中点表示的数为
,线段 AB 的中点表示的数为![]() .
.
【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点 A 出发, 以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒 2个单 位长度的速度向左匀速运动,设运动时间为t秒(t>0).
【综合运用】(1) 填空:
①A、B两点之间的距离AB=__________,线段AB的中点表示的数为_______;
②用含t的代数式表示:t秒后,点P表示的数为_______;点Q表示的数为_____.
(2) 求当t为何值时,P、Q 两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点 P在运动过程中,线段MN的长度是否发 生变化?若变化,请说明理由;若不变,请求出线段MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读第①小题的计算方法,再计算第②小题.
①–5![]() +(–9
+(–9![]() )+17
)+17![]() +(–3
+(–3![]() )
)
解:原式=[(–5)+(–![]() )]+[(–9)+(–
)]+[(–9)+(–![]() )]+(17+
)]+(17+![]() )+[(–3+(–
)+[(–3+(–![]() )]
)]
=[(–5)+(–9)+(–3)+17]+[(–![]() )+(–
)+(–![]() )+(–
)+(–![]() )+
)+![]() ]
]
=0+(–1![]() )
)
=–1![]() .
.
上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000![]() )+(﹣1999
)+(﹣1999![]() )+4000
)+4000![]() +(﹣1
+(﹣1![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 的顶点为A.
的顶点为A.
(1)求点A的坐标;

(2)将线段![]() 沿
沿![]() 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段![]() .
.
①直接写出点![]() 和
和![]() 的坐标;
的坐标;
②若抛物线![]() 与四边形
与四边形![]() 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约能源,某城市开展了节约水电活动,已知该城市共有10000户家庭,活动前,某调查小组随机抽取了部分家庭每月的水电费的开支(单位:元),结果如左图所示频数直方图(每一组含前一个边界值,不含后一个边界值);活动后,再次调查这些家庭每月的水电费的开支,结果如表所示:

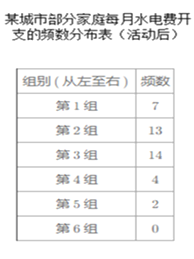
(1)求所抽取的样本的容量;
(2)如以每月水电费开支在225元以下(不含)为达到节约标准,请问通过本次活动,该城市大约增加了多少户家庭达到节约标准?
(3)活动后,这些样本家庭每月水电费开支的总额能否低于6000元?
(4)请选择一个适当的统计量分析活动前后的相关数据,并评价节约水电活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
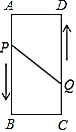
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以2厘米/秒的速度向终点
以2厘米/秒的速度向终点![]() 移动,点
移动,点![]() 以1厘米/秒的速度向
以1厘米/秒的速度向![]() 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为
移动,当有一点到达终点时,另一点也停止运动.设运动的时间为![]() 秒,当
秒,当![]() ________时,以点
________时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.
为顶点的三角形是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com