
【题目】在平面直角坐标系xOy中,抛物线![]() 的顶点为A.
的顶点为A.
(1)求点A的坐标;

(2)将线段![]() 沿
沿![]() 轴向右平移2个单位得到线段
轴向右平移2个单位得到线段![]() .
.
①直接写出点![]() 和
和![]() 的坐标;
的坐标;
②若抛物线![]() 与四边形
与四边形![]() 有且只有两个公共点,结合函数的图象,求
有且只有两个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
【答案】(1)(2,3)(2)![]() (2,0),
(2,0), ![]() (4,3)(3)
(4,3)(3)![]()
【解析】试题分析:(1)将抛物线解析式配成顶点式,即可得出顶点坐标;
(2)根据平移的性质即可得出结论;
(3)结合图象,判断出抛物线和四边形AOO'A'只有两个公共点的分界点即可得出结论.
试题解析:
解:(1)∵y=mx2-4mx+4m+3=m(x2-4x+4)+3=m(x-2)2+3,
∴抛物线的顶点A的坐标为(2,3).
(2)由(1)知,A(2,3),
∵线段OA沿x轴向右平移2个单位长度得到线段O′A′.
∴A'(4,3),O'(2,0);
(3)如图,
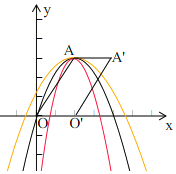
∵抛物线y=mx2-4mx+4m+3与四边形AOO′A′有且只有两个公共点,
∴m<0.
由图象可知,抛物线是始终和四边形AOO'A'的边O'A'相交,
∴抛物线已经和四边形AOO′A′有两个公共点,
∴将(0,0)代入y=mx2-4mx+4m+3中,得m=![]() .
.
∴![]() <m<0.
<m<0.


科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°﹣∠ABD;④∠BDC=∠BAC.其中正确的结论的有__________.(把正确结论的序号都写上去)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求若干个相同的不为零的有理数的除法运算叫做除方.
如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把![]() (a≠0)记作
(a≠0)记作![]() ,读作“a的圈n次方”.
,读作“a的圈n次方”.
(1)直接写出计算结果: ![]() _____,
_____, ![]() _________,
_________, ![]() ___________,
___________,
(2)我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,
请尝试将有理数的除方运算转化为乘方运算,归纳如下:一个非零有理数的圈 n 次方等于_____.
(3)计算 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,b),B(c,0)是x轴正半轴上一点,∠ABO=30°,若![]() 与|2﹣a|互为相反数.
与|2﹣a|互为相反数.

(1)求c的值;
(2)如图2,AC⊥AB交x轴于C,以AC为边的正方形ACDE的对角线AD交x轴于F.
①求证:BE=2OC;
②记BF2﹣OF2=m,OC2=n,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活与数学
日 | 一 | 二 | 三 | 四 | 五 | 六 |
1 | 2 | 3 | 4 | 5 | 6 | |
7 | 8 | 9 | 10 | 11 | 12 | 13 |
14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 |
(1)姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是48,那么这四个数是_______.
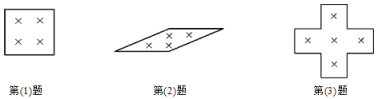
(2)丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是46,则它们分别是_____.
(3)莉也在日历上圈出5个数,呈十字框形,它们的和是55,则中间的数是______.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是______号?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,平面直角坐标系![]() 中点
中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点,连接
三点,连接![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() .
.
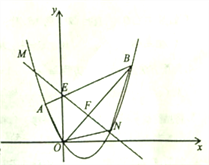
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的函数解析式;
(3)点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 轴右侧),连接
轴右侧),连接![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标并求出四边形
的坐标并求出四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
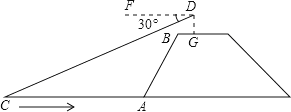
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() =1.73,结果保留两位有效数字)
=1.73,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (m为常数).
(m为常数).
(1)试判断该函数的图象与x轴的公共点的个数;
(2)求证:不论m为何值,该函数的图象的顶点都在函数![]() 的图象上;
的图象上;
(3)若直线y=x与二次函数图象交于A、B两点,当﹣4≤m≤2时,求线段AB的最大值和最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
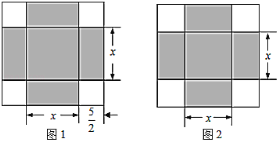
【题目】《代数学》中记载,形如![]() 的方程,求正数解的几何方法是:“如图1,先构造一个面积为
的方程,求正数解的几何方法是:“如图1,先构造一个面积为![]() 的正方形,再以正方形的边长为一边向外构造四个面积为
的正方形,再以正方形的边长为一边向外构造四个面积为![]() 的矩形,得到大正方形的面积为
的矩形,得到大正方形的面积为![]() ,则该方程的正数解为
,则该方程的正数解为![]() .”小聪按此方法解关于
.”小聪按此方法解关于![]() 的方程
的方程![]() 时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
时,构造出如图2所示的图形,已知阴影部分的面积为36,则该方程的正数解为( )
A.6B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com