
| AE |
| AB |
| ||
| 2 |
| ||
| 2 |
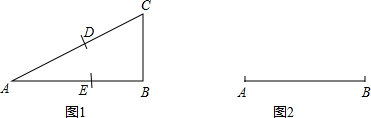
| 5 |
| 5 |
| AE |
| AB |
(
| ||
| 2x |
| ||
| 2 |
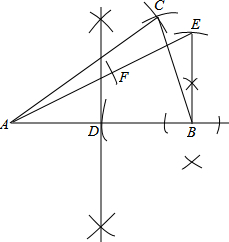 .
.

 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
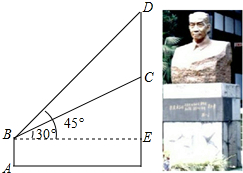 如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:
如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
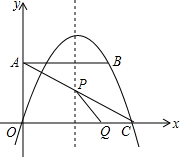 如图,平面直角坐标系中,四边形OABC是直角梯形,AB∥OC,OA=5,AB=10,OC=12,抛物线y=ax2+bx经过点B、C.
如图,平面直角坐标系中,四边形OABC是直角梯形,AB∥OC,OA=5,AB=10,OC=12,抛物线y=ax2+bx经过点B、C.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com