
【题目】已知:如图,点E为□ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF=BE,线段EF与边CD相交于点G.
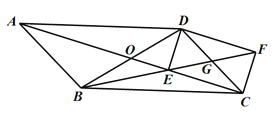
(1)求证:DF//AC;
(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AC=BC,点P在线段BA的延长线上,作PD⊥AC,交AC的延长线于点D,点D关于直线AB的对称点为E,连接PE并延长PE到点F,使EF=AC,连接CF.
(1)依题意补全图1;
(2)求证:AD=CF;
(3)若AC=2,点Q在直线AB上,写出一个AQ的值,使得对于任意的点P总有QD=QF,并证明.
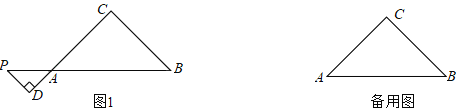
查看答案和解析>>
科目:初中数学 来源: 题型:
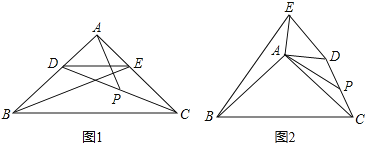
【题目】(问题背景)如图,在![]() 中,
中,![]() ,点D,E分别在边
,点D,E分别在边![]() 上,
上,![]() ,连接
,连接![]() ,点P为
,点P为![]() 的中点.
的中点.
(观察猜想)观察图1,猜想线段![]() 与
与![]() 的数量关系是________,位置关系是________.
的数量关系是________,位置关系是________.
(2)(拓展探究)把![]() 绕点A逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立,请证明:否则写出新的结论并说明理由.
绕点A逆时针方向旋转到图2的位置,(1)中的结论是否仍然成立,若成立,请证明:否则写出新的结论并说明理由.
(3)(问题解决)把![]() 绕点A在平面内自由旋转,若
绕点A在平面内自由旋转,若![]() ,请直接写出线段
,请直接写出线段![]() 长的取值范围.
长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
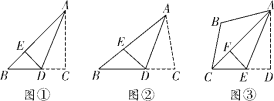
【题目】(1)操作发现
如图①,在![]() 中,
中,![]() ,点D是
,点D是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() ,使得点C恰好落在
,使得点C恰好落在![]() 上的点E处.则
上的点E处.则![]() 的数量关系为______;
的数量关系为______;![]() ________;
________;
(2)问题解决
如图②,若(1)中![]() ,其他条件不变,请猜想
,其他条件不变,请猜想![]() 之间的关系,并证明你的结论;
之间的关系,并证明你的结论;
(3)类比探究
如图③,在四边形![]() 中,
中,![]() ,连接
,连接![]() ,点E是
,点E是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() 使得点D正好落在
使得点D正好落在![]() 上的点F处,若
上的点F处,若![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象由函数
的图象由函数![]() 的图象平移得到,且经过点(1,2).
的图象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当![]() 时,对于
时,对于![]() 的每一个值,函数
的每一个值,函数![]() 的值大于一次函数
的值大于一次函数![]() 的值,直接写出
的值,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com