
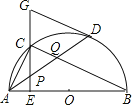
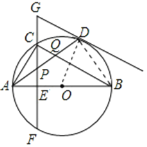
【题目】如图,在⊙O 中,AB 是直径,点 D 是⊙O 上一点,点 C 是弧 AD 的中点,CE⊥AB 于点 E,过点 D 的切线交 EC 的延长线于点 G,连接 AD,分别交 CE,CB 于点 P,Q,连接 AC.
(1)求证:GP=GD.
(2)下列结论:①∠BAD=∠ABC;②点 P 是△ACQ 的外心,其中正确结论是 .(只需填写序号).
【答案】(1)证明见解析;(2)②.
【解析】
连接OD,利用切线的性质,可得出∠GPD=∠GDP,利用等角对等边可得出GP=GD;
(2)由于弧AC 与弧BD不一定相等,根据圆周角定理可知①错误;先由垂径定理得到A为弧CF的中点,再由C为弧AD的中点,得到弧CD=弧AF,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ为直角,由等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,可知②正确;
解:(1)连接OD,
则OD⊥GD,∠OAD=∠ODA,
∵∠ODA+∠GDP=90°,∠EPA+∠EAP=∠EAP+∠GPD=90°,
∴∠GPD=∠GDP;
∴GP=GD;
(2)∵在⊙O中,AB是直径,点D是⊙O上一点,点C是弧AD的中点,
∴弧AC=弧CD≠弧BD,
∴∠BAD≠∠ABC,故①错误;
∵弦CF⊥AB于点E,
∴A为弧CF的中点,即弧AF=弧AC,
又∵C为弧AD的中点,
∴弧AC=弧CD,
∴弧AF=弧CD,
∴∠CAP=∠ACP,
∴AP=CP.
∵AB为圆O的直径,
∴∠ACQ=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P为Rt△ACQ斜边AQ的中点,
∴P为Rt△ACQ的外心,故②正确;
故答案为:②.


科目:初中数学 来源: 题型:
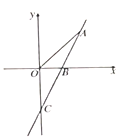
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求![]() 点的坐标和
点的坐标和![]() 的值;
的值;
(2)若点![]() 是直线
是直线![]() 第一象限部分上的一个动点,试写出
第一象限部分上的一个动点,试写出![]() 的面积与
的面积与![]() 的函数关系式;
的函数关系式;
(3)点![]() 在直线
在直线![]() 运动,当点
运动,当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积是
的面积是![]() ?求出此时
?求出此时![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
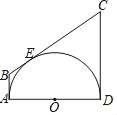
【题目】如图,AB、CD分别与半圆OO切于点A,D,BC切⊙O于点E.若AB=4,CD=9,则⊙O的半径为( )
A. 12 B. ![]()
![]() C. 6 D. 5
C. 6 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
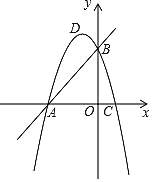
【题目】如图,直线y=x+3与两坐标轴交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)求A、B两点的坐标;
(2)求抛物线的解析式和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
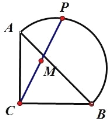
【题目】如图,在等腰 Rt△ABC 中,AC=BC=2,点 P 在以斜边 AB 为直径的半圆上,M 为 PC 的中点.当点 P 沿半圆从点A 运动至点 B 时,点 M 运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,动点E、F分别从D、C两点同时出发,以相同的速度分别在边DC、CB上移动,当点E运动到点C时都停止运动,DF与AE相交于点P,若AD=8,则点P运动的路径长为( )

A. 8![]() B. 4
B. 4![]() C. 4π D. 2π
C. 4π D. 2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市每年都举行“希望杯”篮球赛,去年初赛阶段,共15支队伍参赛,每两队之间都比赛一场,下表是去年初赛部分队伍的积分榜.
队名 | 比赛场次 | 胜场 | 负场 | 积分 |
A | 14 | 10 | 4 | 24 |
B | 14 | 9 | 5 | 23 |
C | 14 | 4 | 10 | 18 |
D | 14 | 0 | 14 | 14 |
(1)去年某队的总积分为20分,则该队在比赛中胜了多少场?
(2)今年,参赛的队伍比去年有所增加,但因场地受限,组委会决定初赛阶段共安排40场比赛,并将参赛队伍平均分成4个小组,各小组每两队之间都比赛一场,求今年比去年增加了多少支队伍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com