
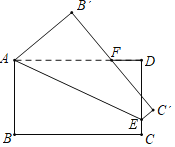
【题目】如图,矩形纸片ABCD中,AB=4,点E在边CD上移动连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′CE,点B、C的对应点分别为点B′、C′
(1)当点E与点C重合时,设B′C′与AD的交点为F,若AD=4DF,则AD=______
(2)若AD=6,B′C′的中点记为P,则DP的取值范围是______
【答案】4![]() 1≤DP≤5.
1≤DP≤5.
【解析】
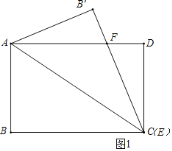
(1)如图1,当点E与点C重合时,易知△AB'C≌△DCA,得到AF=CF,设DF=x,则AD=4x,得AF=CF=AD=DF=3x,Rt△CDF中利用勾股定理解出x,然后得到AD=4x即可 (2)如图2,点P的轨迹是以A为圆心,AP的长为半径的圆上的一段弧,当点E与点D重合时DP的值最大,易得B'P=C'P![]() 6=3,B'A=C'D=4,则AP=DP=5;当点P在AD上时,即在点P'处时,DP的值最小此时,AP=AP'=5,得DP'=AD﹣AP'=6﹣5=1,所以DP的最小值为1,
6=3,B'A=C'D=4,则AP=DP=5;当点P在AD上时,即在点P'处时,DP的值最小此时,AP=AP'=5,得DP'=AD﹣AP'=6﹣5=1,所以DP的最小值为1,
解:∵四边形ABCD为矩形,
∴AB=CD=4,AD∥BC,
∴∠DAC=∠ACB,
如图1,当点E与点C重合时,
由翻折知,△AB'C≌△DCA,
∴∠ACB'=∠ACB,
∴∠DAC=∠ACB',
∴AF=CF,
设DF=x,则AD=4x,
∴AF=CF=AD=DF=3x,
在Rt△CDF中,CF2=DF2+CD2,
∴(3x)2=x2+42,
解得,x1![]() (舍去),x2
(舍去),x2![]() ,
,
∴AD=4x=4![]() ,
,
故答案为:4![]() ;
;
(2)如图2,点P的轨迹是以A为圆心,AP的长为半径的圆上的一段弧,当点E与点D重合时DP的值最大,
∵点P是B'C'的中点,
∴B'P=C'P![]() 6=3,B'A=C'D=4,
6=3,B'A=C'D=4,
∴AP=DP![]() 5,
5,
∴DP的最大值为5,
由图可看出,当点P在AD上时,即在点P'处时,DP的值最小,
此时,AP=AP'=5,
∴DP'=AD﹣AP'=6﹣5=1,
∴DP的最小值为1,
故答案为:1≤DP≤5.



 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的课余生活,陶冶学生的情趣和爱好,某小学开展了学生社团活动。为了解学生参加活动的情况,学校进行了抽样调查,并做了如下的统计图,请根据统计图,完成以下问题
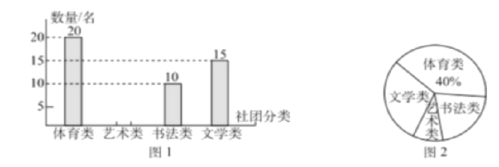
(1)本次调查共抽取了多少名学生?
(2)请补全条形统计图;
(3)若该中学共有![]() 名学生,请你估计该中学最想参加文学社团的学生约有多少名.
名学生,请你估计该中学最想参加文学社团的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
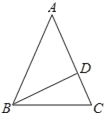
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CDAC;④若AB=2,则BC=![]() ﹣1,其中正确的结论的个数是_____个.
﹣1,其中正确的结论的个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是半圆O的直径,AC是弦,点P沿BA方向,从点B运动到点A,速度为1cm/s,若AB=10cm,点O到AC的距离为4cm.
(1)求弦AC的长;
(2)问经过多长时间后,△APC是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,E是AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止;点Q从点B沿BC运动到点C时停止,速度均为每秒1个单位长度.如果点P、Q同时开始运动,设运动时间为t,△BPQ的面积为y,已知y与t的函数图象如图②所示,以下结论:①BC=10;②cos∠ABE=![]() ;③当0≤t≤10时,y=
;③当0≤t≤10时,y=![]() t2;④当t=12时,△BPQ是等腰三角形;⑤当14≤t≤20时,y=110﹣5t,其中正确的有( )
t2;④当t=12时,△BPQ是等腰三角形;⑤当14≤t≤20时,y=110﹣5t,其中正确的有( )
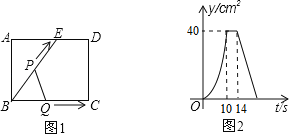
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进![]() 、
、![]() 两种粽子1100个,购买
两种粽子1100个,购买![]() 种粽子与购买
种粽子与购买![]() 种粽子的费用相同,已知
种粽子的费用相同,已知![]() 粽子的单价是
粽子的单价是![]() 种粽子单价的1.2倍.
种粽子单价的1.2倍.
(1)求![]() 、
、![]() 两种粽子的单价各是多少?
两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买![]() 、
、![]() 两种粽子共2600个,已知
两种粽子共2600个,已知![]() 、
、![]() 两种粽子的进价不变,求
两种粽子的进价不变,求![]() 中粽子最多能购进多少个?
中粽子最多能购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
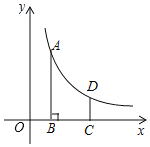
【题目】如图,反比例函数y=![]() (x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=
(x>0)的图象上一点A(m,4),过点A作AB⊥x轴于B,CD∥AB,交x轴于C,交反比例函数图象于D,BC=2,CD=![]() .
.
(1)求反比例函数的表达式;
(2)若点P是y轴上一动点,求PA+PB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com