
 如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE
如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE分析 (1)根据AC为⊙O的直径,得出△BCD为Rt△,通过已知条件证明△BCD∽△BAC即可;
(2)连结DO,如图,根据直角三角形斜边上的中线性质,由∠BDC=90°,E为BC的中点得到DE=CE=BE,则利用等腰三角形的性质得∠EDC=∠ECD,∠ODC=∠OCD,由于∠OCD+∠DCE=∠ACB=90°,所以∠EDC+∠ODC=90°,即∠EDO=90°,于是根据切线的判定定理即可得到DE与⊙O相切.
解答 (1)证明:∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠BDC=90°,
又∵∠ACB=90°,
∴∠ACB=∠BDC,
又∵∠B=∠B,
∴△BCD∽△BAC;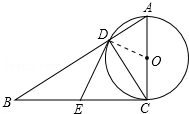 (2)连结DO,如图,
(2)连结DO,如图,
∵∠BDC=90°,E为BC的中点,
∴DE=CE=BE,
∴∠EDC=∠ECD,
又∵OD=OC,
∴∠ODC=∠OCD,
而∠OCD+∠DCE=∠ACB=90°,
∴∠EDC+∠ODC=90°,即∠EDO=90°,
∴DE⊥OD,
∴DE与⊙O相切.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了直角三角形斜边上的中线性质和相似三角形的判定与性质.


科目:初中数学 来源: 题型:解答题
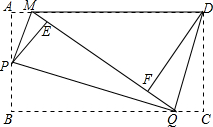 如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k<$\frac{1}{3}$ | B. | k>$-\frac{1}{3}$ | C. | k<$\frac{1}{3}$且k≠0 | D. | k>$-\frac{1}{3}$且k≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
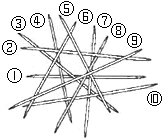 挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走.如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走( )
挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走.如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走( )| A. | ②号棒 | B. | ⑦号棒 | C. | ⑧号棒 | D. | ⑩号棒 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com