
����Ŀ���Ķ����ϣ����ǰѶ�����Բ�ϣ�����һ�ߺ�Բ�ཻ����һ�ߺ�Բ���еĽǽ������нǣ���ͼ1��ABC��ʾ��ͬѧ���о����֣�PΪԲ������һ�㣬����AC����Բ��Oʱ����AB�С�O�ڵ�A����ʱ���нǡ�CAB=��P��ͼ2��
֤������AB�С�O�ڵ�A�����CAB=90�㣬�֡�AC��ֱ�������P=90����CAB=��P
������չ����AC������Բ��O����ͼ3�����ý��ۣ����нǡ�CAB=��P����������˵�����ɣ�
֪ʶ���ã���ͼ4��AD�ǡ�ABC�С�BAC��ƽ���ߣ�������A�ġ�O��BC���ڵ�D����AB��AC�ֱ��ཻ��E��F����֤��EF��BC��
���𰸡��⣺������չ��������
��ͼ3������AO���ӳ�����O�ڵ�D������CD��
���D=��P��
��AD��ֱ����
���D+��CAD=90�㣬
�֡�AB��Բ�ڵ�A��
���CAB+��CAD=90�㣬
���CAB=��CAD��
����CAD=��P��
���CAB=��P��
֪ʶ���ã���ͼ4������DF��
��AD�ǡ�ABC�С�BAC��ƽ���ߣ�
���EAD=��DAC��
�ߡ�O��BC���ڵ�D��
���FDC=��DAC��
���FDC=��EAD��
���ڡ�O�С�EAD=��EFD��
���FDC=��EFD��
��EF��BC��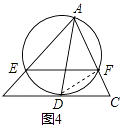
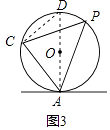
��������������չ����������AO���ӳ�����O�ڵ�D������CD����Բ�ܽǶ����ɵá�D=��P������AD��ֱ����AB��Բ�ڵ�A����֤�á�CAB=��CAD���̶�֤�ý��ۣ�
֪ʶ���ã�����DF��AD�ǡ�ABC�С�BAC��ƽ���ߣ���O��BC���ڵ�D���ɵá�FDC=��EAD������Բ�ܽǶ����ɵá�EAD=��EFD���̶�֤�ý��ۣ�
�����㾫����������Ĺؼ������������ߵ����ʶ��������֪ʶ���������ߵ����ʣ�1�������е㴹ֱ�������뾶��ֱ����Բ������2�������е㴹ֱ�����ߵ�ֱ�߱ؾ���Բ��3��Բ�����ߴ�ֱ�ھ����е�İ뾶��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x��һԪ���η���tx2����3t+2��x+2t+2=0��t��0��
��1����֤����������������ȵ�ʵ������
��2���跽�̵�����ʵ�����ֱ�Ϊx1 �� x2������x1��x2������y�ǹ���t�ĺ�������y=x2��2x1 �� ����������Ľ���ʽ������������ͼ��
��3���۲죨2���еĺ���ͼ��y��2tʱ��д���Ա���t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ�
��ac��0 ��2a+b=0 ��4a+2b+c��0 �ܶ�����ʵ��x����ax2+bx��a+b
��ȷ�Ľ������Ϊ�� �� 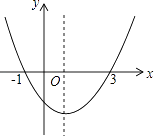
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
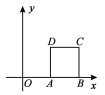
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪A(1��0)��B(2��0)���ı���ABCD�������Σ�
(1)д��C��D�������ꣻ
(2)��������ABCD��O����ʱ����ת90��������ı��ε��ĸ����������ֱ��Ƕ��٣�
(3)����(2)���õ��ı�������O����ʱ����ת90��������ı��ε��ĸ����������ֱַ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʩ�����ذ�����һ��Բ������ˮͰ��ľ��֧�ܣ���ͼ1����������ľ���ĺ�ȣ��丩��ͼ��ͼ2��ʾ����֪AD��ֱƽ��BC��AD=BC=48cm����Բ������ˮͰ�ĵ���뾶�����ֵ��cm�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڸ��ʣ�����˵����ȷ���ǣ� ��
A.���ء����콵��ĸ�����75%�������������ػ���75%��ʱ�������
B.�������һö�ʵؾ��ȵ�Ӳ�ң���غ�һ����������
C.��һ�γ齱��У��н��ĸ�����1%����齱100�ξ�һ�����н�
D.ͬʱ������ö�ʵؾ���Ӳ�ң���һöӲ���������ϣ�һöӲ�ҷ������ϡ��ĸ����� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
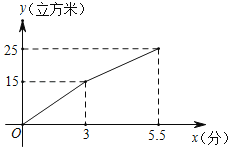
����Ŀ��ij��ˮ�ഢ�������Ϊ25�����ף�����һ������ں�һ������ڣ���ijʱ�̿�ʼ��ֻ������ڣ����������ע��ˮ�࣬3���Ӻ��ٴ�����ڣ����������䳵���ˮ�࣬�־���2.5���Ӵ����ע�����ر�����ڣ�����ԭ��������ٶȼ��������䳵���ˮ�࣬�������ˮ�������ﵽ8������ʱ���ر�����ڣ�������ڵ�ˮ����y�������ף���ʱ��x���֣�֮��IJ��ֺ���ͼ����ͼ��ʾ��
��1����ÿ���������ע���ˮ������
��2����3��x��5.5ʱ����y��x֮��ĺ�����ϵʽ��
��3�������ÿ���������䳵�����ˮ�������� �������ף��Ӵ�����ڵ��ر�����ڹ��õ�ʱ��Ϊ�� �����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�O�У���AB���Ե��ӻ���Բ�ܳ��� ![]() ������Բ�İ뾶Ϊ4cm����
������Բ�İ뾶Ϊ4cm���� 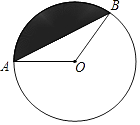
��1����AB�ij���
��2������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��������AEFG��һ��������A����G��E�ֱ����߶�AD��AB�ϣ� 
��1������DF��BF������������AEFG�Ƶ�A��˳ʱ�뷽����ת���ж����⡰����ת�Ĺ����У��߶�DF��BF�ij�ʼ����ȡ��Ƿ���ȷ���� ��
��2������������AEFG�Ƶ�A��˳ʱ�뷽����ת������DG������ת�����У����ܷ��ҵ�һ���߶εij����߶�DG�ij�ʼ����ȣ�����ͼΪ��˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com