
 )在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?
)在直线MG上。问:当m为何值时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形?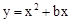 。
。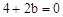 ,解得
,解得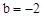 。
。 。
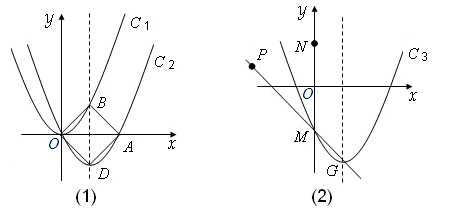
。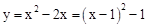 ,∴抛物线C2的顶点D的坐标为(1,
,∴抛物线C2的顶点D的坐标为(1,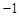 )。
)。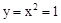 ,∴点B的坐标为(1,1)。
,∴点B的坐标为(1,1)。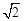 。∴四边形ODAB是菱形。
。∴四边形ODAB是菱形。 。
。 中令x=0,得
中令x=0,得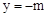 ,∴M
,∴M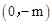 。
。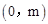 。∴MN=
。∴MN= 。
。 和P(
和P( )得Q(
)得Q(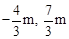 )。
)。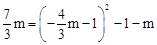 ,解得
,解得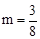 或
或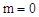 (舍去)。
(舍去)。 )。
)。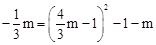 ,解得
,解得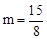 或
或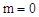 (舍去)。
(舍去)。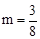 或
或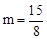 时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形。
时,在抛物线C3上存在点Q,使得以M、N、P、Q为顶点的四边形为平行四边形。

科目:初中数学 来源:不详 题型:单选题
 上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为
上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为
A. | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作直线CP的垂线,垂足分别为D、E,连接点MD、ME.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
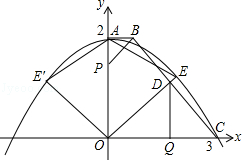
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,同理
,同理 ,所以AB的中点坐标为
,所以AB的中点坐标为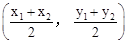 .由勾股定理得
.由勾股定理得 ,所以A、B两点间的距离公式为
,所以A、B两点间的距离公式为 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.a<0,b<0,c>0,b2﹣4ac>0 | B.a>0,b<0,c>0,b2﹣4ac<0 |
| C.a<0,b>0,c<0,b2﹣4ac>0 | D.a<0,b>0,c>0,b2﹣4ac>0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.①② | B.②③ | C.①②④ | D.①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com