
 ,∠C=45°,P为BC边上的动点,过P作PD∥AB交AC于点
,∠C=45°,P为BC边上的动点,过P作PD∥AB交AC于点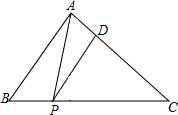 D,连接AP,△ABP,△APD,△CDP的面积分别记为S1,S2,S3,设BP=x.
D,连接AP,△ABP,△APD,△CDP的面积分别记为S1,S2,S3,设BP=x.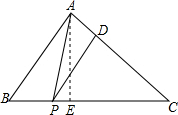 解:(1)过A作AE⊥BC,则AE为BC边上的高,
解:(1)过A作AE⊥BC,则AE为BC边上的高, ,∠C=45°,得到此三角形为等腰直角三角形,
,∠C=45°,得到此三角形为等腰直角三角形, ,即AE=ACsin45°=4
,即AE=ACsin45°=4 ×
× =4,
=4, ;
; ,
,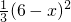 =
=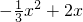 ;
;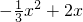 =
= =
= ,
, 即可求出用x的代数式分别表示S1,S2,S3;
即可求出用x的代数式分别表示S1,S2,S3;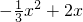 利用配方法即可求出△APD的面积最大值;
利用配方法即可求出△APD的面积最大值;

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com