
【题目】如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.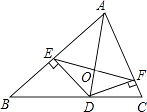
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.
【答案】
(1)
证明:
∵AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,
∴DE=DF(角平分线的性质)
(2)
解:垂直.理由如下:
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
 ,
,
∴Rt△AED≌Rt△AFD(AAS),
∴AE=AF,
∴点A在线段EF的垂直平分线上,
同理点D也在线段EF的垂直平分线上,
∴AD⊥EF
(3)
解:设S△CDF=x,则S△BDE=2x,
∵S△ACD=1,且△AED≌△AFD,
∴S△AED=S△AFD=1﹣x,
∴S△ABD=S△BDE+S△AED=2x+1﹣x=x+1,
又S△ABD= ![]() ABDE,S△ACD=
ABDE,S△ACD= ![]() ACDF,且AB=c,AC=b,
ACDF,且AB=c,AC=b,
∴ ![]() ×cDE=x+1,
×cDE=x+1, ![]() ×bDF=1,
×bDF=1,
∴DE= ![]() ,DF=
,DF= ![]() ,
,
又由(1)可知DE=DF,
∴ ![]() =
= ![]() ,解得x=
,解得x= ![]() ﹣1,
﹣1,
∵△AED≌△AFD,
∴S△AED=S△AFD=S△ACD﹣S△CDF=1﹣x,
∴S四边形AEDF=2S△AED=2(1﹣x)=2[1﹣( ![]() ﹣1)]=4﹣
﹣1)]=4﹣ ![]() ,
,
即四边形AEDF的面积为4﹣ ![]()
【解析】(1)由角平分线的性质直接可得到DE=DF;(2)可证明△AED≌△AFD,可知AE=AF,利用线段垂直平分线的判定可证明AD是EF的垂直平分线,可证得结论;(3)设△CDF的面积为x,则可分别表示出△BED、△ADE的面积,利用三角形的面积可分别表示出DE和DF,根据DE=DF可得到关于x的方程,可求得x的值,进一步可求得四边形AEDF的面积.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:
【题目】某班5名学生在一次数学测试中的成绩以90为标准,超过的分数记为正数,不足的分数记为负数,记录如下:-4,+9,-1, 0,+6,则他们的平均成绩是 ________分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段CD,按要求画出图形并计算:延长线段CD到B,使得DB= ![]() CB,延长DC到点A,使AC=2DB,若AB=8cm,求出CD与AD的长.
CB,延长DC到点A,使AC=2DB,若AB=8cm,求出CD与AD的长. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,D是线段CB的中点,已知图中所有的线段的长度之和为23,线段AC的长度与线段CB的长度都是正整数,则线段AC长 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在x轴的正半轴上,且OA1=2,OA2=2OA1,OA3=2OA2,…,OAn=2OAn﹣1,点B1,B2,B3,…,Bn在第一象限的角平分线l上,且A1B1,A2B2,…,AnBn都与射线l垂直,则B1的坐标是 ,B3的坐标是 ,Bn的坐标是 .
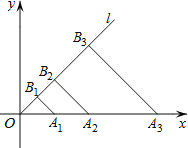
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com