
| 板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
| 甲型 | 108 | 61 | 12 |
| 乙型 | 156 | 51 | 10 |
分析 (1)设安排x人生产A种板材,则安排(210-x)人生产B种板材,根据工作时间相等建立方程求出其解即可;
(2)设建甲型y间,则建乙型(400-y)间,根据条件建立不等式组求出其解就可以得出结论;根据板房的数量和每间住人的数量就可以不少于需要安置的人数建立不等式就可以求出结论.
解答 解:(1)设安排x人生产A种板材,则安排(280-x)人生产B种板材根据题意,得$\frac{48000}{60x}$=$\frac{24000}{40(210-x)}$,
解得:x=120,
经检验,x=120是原方程的根,
生产B种板材的人数为:210-x=90人,
答:安排120人生产A种板材,安排90人生产B种板材,才能确保同时完成各自的生产任务;
(2)设建甲型y间,则建乙型(400-y)间,能安置M人,
根据题意,得$\left\{\begin{array}{l}{108y+156(400-y)≤48000}\\{61y+51(400-y)≤24000}\end{array}\right.$,
解得:300≤y≤360.
∵y是整数
∴符合条件的y值有61个,
∴共有61种建房方案可供选择;
根据题意,安置人数M=12y+10(400-y)=2y+4000(300≤y≤360),
∵2>0,∴M随y的增大而增大,
∴y=360时安置人数最多,
∴400-y=40,
∴建甲型360间,建乙型40间时,能最多地安置灾民.
M=2y+4000=2×360+4000=4720,
答:这400间板房的搭建共有61种方案;建甲型360间,建乙型40间时,能最多地安置灾民;最多能安置灾民4720人.
点评 本题考查了列分式方程解工程问题的运用,列一元一次不等式组解设计方案题型的运用,列一元一次不等式解实际问题的运用及分式方程与不等式组及不等式的解法的运用,解答时认真分析理清题目中的数量关系是关键.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:选择题
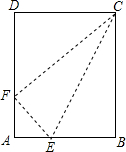 如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )
如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
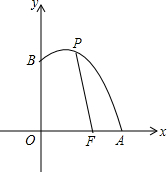 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20×108 | B. | 2×108 | C. | 0.2×108 | D. | 2×107 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com