
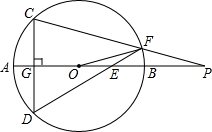
 如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.
如图,已知AB是⊙O的直径,点E在线段AB上,CD⊥AB于G,连接DE交⊙O于F,连接CF交AB延长线于P.分析 延长FO并交⊙O于Q,连接DQ,根据已知条件得出∠QFD+∠Q=90°和∠P+∠C=90°,再根据圆周角定理得出∠Q=∠C,求出∠QFD=∠P,从而得出△FOE∽△POF,即可得出OF2=OE•OP.
解答 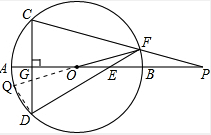 解:延长FO并交⊙O于Q,连接DQ,
解:延长FO并交⊙O于Q,连接DQ,
∵FQ是⊙O直径,
∴∠FDQ=90°,
∴∠QFD+∠Q=90°,
∵CD⊥AB,
∴∠P+∠C=90°,
∵∠Q=∠C,
∴∠QFD=∠P.
∵∠FOE=∠POF,
∴△FOE∽△POF,
∴$\frac{OE}{OF}$=$\frac{OF}{OP}$,
∴OF2=OE•OP.
点评 此题考查了相似三角形的判定与性质,用到的知识点是圆周角定理相似三角形的判定与性质,关键是根据题意求出∠QFD=∠P.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
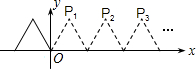 如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
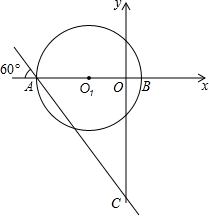 在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.
在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
| 甲型 | 108 | 61 | 12 |
| 乙型 | 156 | 51 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
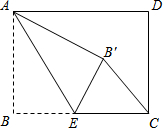 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 855.6×108 | B. | 8.556×108 | C. | 8.556×1011 | D. | 8.556×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
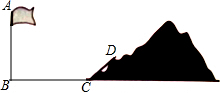 如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).
如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
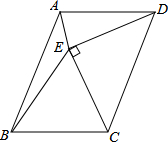 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )| A. | 120° | B. | 135° | C. | 150° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com