
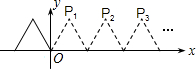
 如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$). 分析 根据等边三角形的性质易求得P1的坐标为(1,$\sqrt{3}$),在等边三角形翻折的过程中,P点的纵坐标不变,而每翻折一次,横坐标增加2个单位(即等边三角形的边长),可根据这个规律求出点P2015的坐标.
解答 解:∵边长为2的等边三角形,
∴P1(1,$\sqrt{3}$),
而P1P2=P2P3=2,
∴P2(3,$\sqrt{3}$),P3(5,$\sqrt{3}$);
依此类推,Pn(1+2n-2,$\sqrt{3}$),即Pn(2n-1,$\sqrt{3}$);
当n=2015时,P2015(4029,$\sqrt{3}$).
故答案为:(4029,$\sqrt{3}$).
点评 本题主要考查了规律型问题,通常要根据简单的条件得到一般化规律,然后根据规律求特定的值,难度适中.


科目:初中数学 来源: 题型:解答题
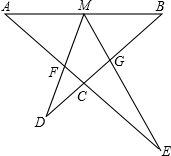 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
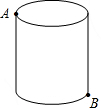 如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?
如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
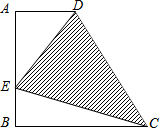 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
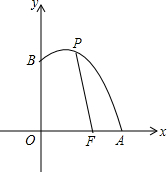 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
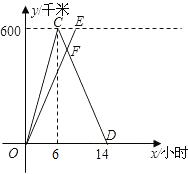 已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com