
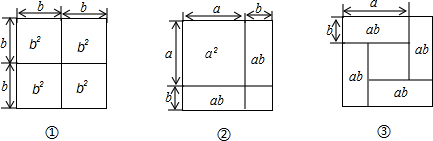
分析 (1)根据面积的和差,可得答案;
(2)①根据面积的和差,可得答案;
②根据长方形的面积公式,可得方程,根据解方程,可得长方形的长、宽,根据长方形的周长公式,可得答案.
解答 解:(1)如图②可以解释恒等式a2+2ab+b2=(a+b)2;
(2)①用面积关系写出一个代数恒等式(a+b)2-(a-b)2=4ab;
故答案为:(a+b)2,(a+b)2-(a-b)2=4ab;
②设长方形的宽为x,长为(x+3),由题意,得
x(x+3)=3.
解得 x=$\frac{-3+\sqrt{21}}{2}$,长$\frac{\sqrt{21}+3}{2}$,
长方形的周长($\frac{\sqrt{21}+3}{2}$+$\frac{\sqrt{21}-3}{2}$)×2=2$\sqrt{21}$.
点评 本题考查了完全平方公式,利用面积的和差得出完全平方公式是解题关键.


科目:初中数学 来源: 题型:解答题
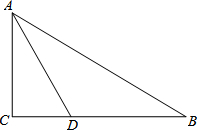 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
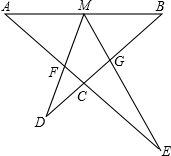 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
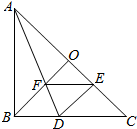 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①图中有4对全等三角形;②若将△DEF沿EF折叠,则点D不一定落在AC上;③BD=BF;④S四边形DFOE=S△AOF,上述结论中正确的个数是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF.下列结论:①图中有4对全等三角形;②若将△DEF沿EF折叠,则点D不一定落在AC上;③BD=BF;④S四边形DFOE=S△AOF,上述结论中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
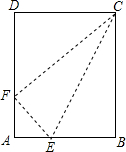 如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )
如图,小明将一块矩形纸片ABCD沿CE折叠,B点恰好落在AD边上,设此点为F,若AB:BC=3:5,则sin∠EFA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
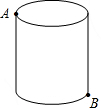 如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?
如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
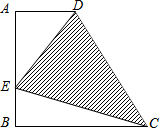 如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:
如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E.设BE=x,△DEC的面积为y,问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com