
分析 把A、B两点横坐标分别代入解析式,求出纵坐标,又因为△AOB是直角三角形,可以利用勾股定理列出关于a的方程,求出a的值,便可利用勾股定理求出各边长.
解答 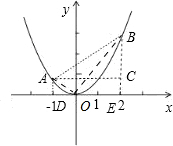 解:如图所示:过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,作AC⊥BE于C.
解:如图所示:过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,作AC⊥BE于C.
将x=-1、x=2分别代入解析式得,yA=a,yB=4a.
于是BC=4a-a=3a,AC=2-(-1)=3,
所以AB2=(3a)2+32=9a2+9,
又因为在Rt△ADO中,AO2=a2+1,
在Rt△BOE中,OB2=22+(4a)2
当∠AOB=90°时,根据勾股定理,AB2=AO2+BO2
即9a2+9=a2+1+22+(4a)2,解得a=$\frac{\sqrt{2}}{2}$(负值不合题意舍去),
于是AO2=$\frac{1}{2}$+1=$\frac{3}{2}$,AO=$\frac{\sqrt{6}}{2}$,
OB2=22+8=12,OB=2$\sqrt{3}$,
AB2=AO2+BO2=$\frac{3}{2}$+12=$\frac{27}{2}$,AB=$\frac{3\sqrt{6}}{2}$;
当∠OAB=90°时,AB2+AO2=BO2,即9a2+9+a2+1=22+(4a)2,解得a=1,
于是OA=$\sqrt{2}$,OB=2$\sqrt{5}$,AB=3$\sqrt{2}$,
当∠OBA=90°时,AB2=AO2-BO2,即9a2+9=a2+1-[22+(4a)2],无解;
综上所述,AB的长度为:$\frac{3\sqrt{6}}{2}$或3$\sqrt{2}$.
故答案是:$\frac{3\sqrt{6}}{2}$或3$\sqrt{2}$.
点评 本题考查了二次函数图象上点的坐标特征.解答此题的关键是作出辅助线,利用勾股定理建立起关于参数a的关系式,再求出各边长,将它们相加即可求出周长.


科目:初中数学 来源: 题型:选择题
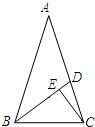 如图,等腰△ABC中,∠A=36°,∠ABC的平分线交AC于D,过点C作CE⊥BD,交BD于点E,则$\frac{DE}{BE}$的值为( )
如图,等腰△ABC中,∠A=36°,∠ABC的平分线交AC于D,过点C作CE⊥BD,交BD于点E,则$\frac{DE}{BE}$的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\sqrt{5}$-2 | C. | $\frac{3-\sqrt{5}}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
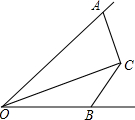 如图,在∠AOB中,OC平分∠AOB,OA>OB,∠OAC+∠OBC=180°,则AC与BC之间的大小关系是( )
如图,在∠AOB中,OC平分∠AOB,OA>OB,∠OAC+∠OBC=180°,则AC与BC之间的大小关系是( )| A. | AC=BC | B. | AC>BC | C. | AC<BC | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
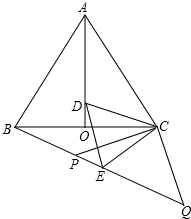 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com