
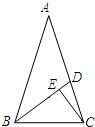
 如图,等腰△ABC中,∠A=36°,∠ABC的平分线交AC于D,过点C作CE⊥BD,交BD于点E,则$\frac{DE}{BE}$的值为( )
如图,等腰△ABC中,∠A=36°,∠ABC的平分线交AC于D,过点C作CE⊥BD,交BD于点E,则$\frac{DE}{BE}$的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\sqrt{5}$-2 | C. | $\frac{3-\sqrt{5}}{2}$ | D. | $\frac{1}{3}$ |
分析 根据角平分线的性质以及已知条件推知∠C=∠C,∠A=∠CBD=36°,所以△CED∽△BCD;然后根据相似三角形的对应边成比例求得CD:DE=BD:CE;最后设ED=x,BD=BC=a,从而得到BC=BD,则BE=CE=CD=a-x,利用BE2=BD•ED得到有关x的方程,用a表示出有关的线段,求线段的比即可.
解答 解:在等腰△ABC中,∠A=36°
∴∠ABC=∠ACB=72°
∵BD平分∠ABC
∴∠ABD=∠CBD=36°
同理∠DCE=∠BCE=36°
∴∠DEC=36°+36°=72°,∠BDC=72°
∴△CED∽△BCD
故:CD:DE=BD:CE,
设ED=x,BD=BC=a,
∵BC=BD,则BE=CE=CD=a-x,
故BE2=BD•ED,即(a-x)2=ax,
移项合并同类项得x2-3ax+a2=0,
解得x=$\frac{3-\sqrt{5}}{2}$a,或x=$\frac{3+\sqrt{5}}{2}$a>BD(舍去)
∴$\frac{DE}{BE}$=$\frac{x}{a-x}$=$\frac{\frac{3-\sqrt{5}}{2}a}{a-\frac{3-\sqrt{5}}{2}a}$=$\frac{\sqrt{5}-1}{2}$,
故选A.
点评 本题主要考查相似三角形的判定和相似三角形对应边成比例,解题的关键是从复杂的图形中找到相似的三角形,难度中等.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
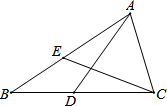 如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.
如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
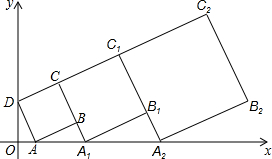 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )| A. | 5($\frac{3}{2}$)2010 | B. | 5($\frac{9}{4}$)2010 | C. | 5($\frac{9}{4}$)2011 | D. | 5($\frac{3}{2}$)2011 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
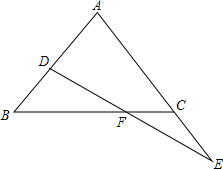 如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.
如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com