
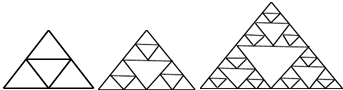
分析 由图可以看出:第一个图形中5个正三角形,第二个图形中5×3+2=17个正三角形,第三个图形中17×3+2=53个正三角形,由此得出第四个图形中53×3+2=161个正三角形,第五个图形中161×3+2=485个正三角形,进一步类推得出答案即可.
解答 解:第一个图形正三角形的个数为5,
第二个图形正三角形的个数为5×3+2=17,
第三个图形正三角形的个数为17×3+2=53,
第四个图形正三角形的个数为53×3+2=161,
第五个图形正三角形的个数为161×3+2=485,
第六个图形正三角形的个数为485×3+2=1457.
故答案为:1457.
点评 此题考查图形的变化规律,找出数字与图形之间的联系,找出规律解决问题.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:填空题
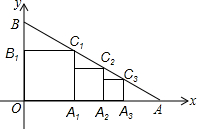 如图,在平面直角坐标系中,点A($\sqrt{3}$,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为$(\frac{3-\sqrt{3}}{2})^{n}$.
如图,在平面直角坐标系中,点A($\sqrt{3}$,0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为$(\frac{3-\sqrt{3}}{2})^{n}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
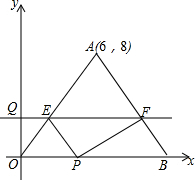 如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).
如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
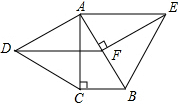 如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.
如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
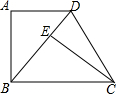 如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•
如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有最小值$\frac{3}{4}$,但无最大值 | B. | 有最小值$\frac{3}{4}$,有最大值1 | ||
| C. | 有最小值1,有最大值$\frac{19}{4}$ | D. | 无最小值,也无最大值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com