
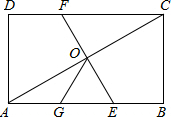
 如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( )
如图,在矩形ABCD中,O为AC的中点,EF过O点且EF⊥AC分别交DC于E,交AB于E,点G是AE的中点,且∠AOG=30°,则下列结论:(1)DC=3OG;(2)OG=$\frac{1}{2}$BC;(3)四边形AECF为菱形;(4)S△AOE=$\frac{1}{6}$S四边形ABCD.其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据条件,OG是直角△AOE斜边上的中线,且△FOC≌△EOA,然后利用三角函数求得BC、AB以及OA、OC之间的关系即可作出判断.
解答 解:∵EF⊥AC,G是AF的中点,
∴AG=OG=GF,
∴∠OAF=∠AOG=30°,
在直角△ABC中,∠CAB=30°,
∴BC=$\frac{1}{2}$AC=OC,设BC=a,AC=2a,AO=OC=a.
AE=$\frac{2\sqrt{3}}{3}$a,AB=$\sqrt{3}$a,OG=$\frac{\sqrt{3}}{3}$a,
∴CD=AB=3OG,故①正确;
OG=$\frac{\sqrt{3}}{3}$a≠$\frac{1}{2}$a=$\frac{1}{2}$BC,故②错误;
易证△FOC≌△EOA,
∴OE=OF,
又∵AO=OC,EF⊥AC,
∴四边形AFCE是菱形,故③正确;
∵S△AOE=$\frac{1}{2}$a•$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{6}$a2,S矩形ABCD=a•$\sqrt{3}$a=$\sqrt{3}$a2,
∴S△AOE=$\frac{1}{6}$S矩形ABCD,故④正确.
故选C.
点评 本题考查了矩形的性质以及菱形的判定,正确理解图形中∠CAB=30°,从而确定BC、AB以及OA、OC之间的关系是关键.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
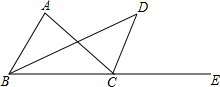 如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
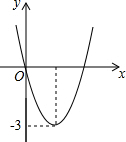 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的取值范围是( )| A. | m≤3 | B. | m≥3 | C. | m≤-3 | D. | m≥-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com