
【题目】如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为_____.

【答案】![]() 或1.
或1.
【解析】
由题意DE=EC=EC′=1,由三角形三条边的关系可知DC′≠DA,所以只要分两种情形讨论即可:①如图1中,当AD=AC′=2时,连接AE.先证△ADE≌△AC′E,再在Rt△ABF中利用勾股定理列方程求解即可;②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件,此时CF=1.
由题意DE=EC=EC′=1,
∴DC′<1+1
∴DC′≠DA,只要分两种情形讨论即可:
①如图1中,当AD=AC′=2时,连接AE.
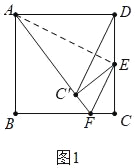
∵AE=AE,AD=AC′,DE=DC′,
∴△ADE≌△AC′E,
∴∠ADE=∠AC′E=90°,
∵∠C=∠FC′E=90°,
∴∠AC′E+∠FC′E=180°,
∴A、C′、F共线,设CF=x,则BF=2﹣x,AF=2+x,
在Rt△ABF中,22+(2﹣x)2=(2+x)2,
解得x=![]() .
.
②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件,此时CF=1.

综上所述,满足条件的CF的长为![]() 或1.
或1.
故答案为![]() 或1.
或1.


科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级500名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组:A组:37.5~42.5,B组:42.5~47.5,C组:47.5~52.5,D组:52.5~57.5,E组:57.5~62.5,并依据统计数据绘制了如下两个不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ;在扇形统计图中D组的圆心角是 度.
(2)抽取的学生体重中位数落在 组;
(3)请你估计该校八年级体重超过52kg的学生大约有多少名?
(4)取每个小组的组中值作为本组学生的平均体重(A组的组中值为![]() ),请你估计该校八年级500名学生的平均体重.
),请你估计该校八年级500名学生的平均体重.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有8×8的正方形网格,每个小正方形边长为1,按要求操作并计算。
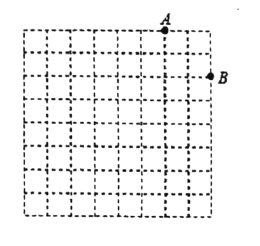
(1)在8×8的正方形网格中建立平面直角坐标系,使点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)将点![]() 向下平移5个单位,再关于
向下平移5个单位,再关于![]() 轴对称得到点
轴对称得到点![]() ,则点
,则点![]() 坐标为(_______,_________);
坐标为(_______,_________);
(3)画出三角形![]() ,并求其面积。
,并求其面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某班数学兴趣小组利用数学知识测量建筑物DEFC的高度.他们从点A出发沿着坡度为i=1:2.4的斜坡AB步行26米到达点B处,此时测得建筑物顶端C的仰角α=35°,建筑物底端D的俯角β=30°.若AD为水平的地面,则此建筑物的高度CD约为( )米.(参考数据:![]() ≈1.7,tan35°≈0.7)
≈1.7,tan35°≈0.7)

A. 23.1 B. 21.9 C. 27.5 D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=![]() (m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=
(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=![]() ,OA=2.
,OA=2.
(1)求反比例函数和一次函数的解析式;
(2)点D是反比例函数图象在第三象限部分上的一点,且到x轴的距离是3,连接AD、BD,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直角△ABC 中,AC=BC,∠C=90°,∠CAB=∠ABC=45°,过点 B 作射线BD⊥AB 于 B,点 P 为 BC 边上任一点,在射线上取一点 Q,使得 PQ=AP.
(1)请依题意补全图形;
(2)试判断 AP 和 PQ 的位置关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
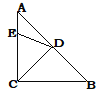
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com