
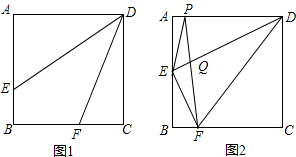
分析 (1)延长BC至点G,使CG=AE,连接DG,根据已知条件和则SAS证出△ADE≌△CDG,得出∠ADE=∠CDG,∠AED=∠G,再根据DE平分∠ADF,得出∠CDG=∠EDF,从而得出∠AED=∠CDE,再根据∠CDE=∠CDF+∠EDF,∠FDG=∠CDF+∠CDG,得出∠FDG=∠CDE=∠G,即可得出AE+CF=DF;
(2)延长DE、CE相交于点M,先证出FE垂直平分DM,得出EM=ED,再根据$\frac{EQ}{EF}$=$\frac{1}{3}$,求出EF的长,从而求出△EQF的面积,根据AAS证出△ADE≌△BME,得出AE=BE,求出tan∠ADE和tan∠EDF,从而得出ED的长,求出$\frac{PQ}{QF}$,
最后根据S△PEQ:S△FEQ=PQ:QG,即可求出△QEP的面积.
解答 解:(1)延长BC至点G,使CG=AE,连接DG,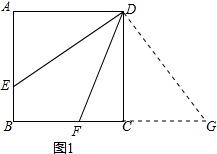
∵四边形ABCD是正方形,
∴AD=DC,
在△ADE和△CDG中,
$\left\{\begin{array}{l}{AD=DC}\\{∠DAE=∠DCG}\\{CG=AE}\end{array}\right.$,
∴△ADE≌△CDG(SAS),
∴∠ADE=∠CDG,∠AED=∠G,
∵∠ADE=∠EDF,
∴∠CDG=∠EDF,
∵AB∥CD,
∴∠AED=∠CDE,
∵∠CDE=∠CDF+∠EDF,∠FDG=∠CDF+∠CDG,
∴∠FDG=∠CDE=∠G,
∴DF=FG=CF+CG=CF+AE;
(2)延长DE、CE相交于点M,
∴∠M=∠ADE=∠FDE,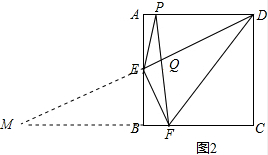
∴FM=FD,
∵FE平分∠BFD,
∴FE垂直平分DM,
∴EM=ED,
∵tan∠EFQ=$\frac{1}{3}$,
∴$\frac{EQ}{EF}$=$\frac{1}{3}$,
∴EF=3EQ=$\frac{3\sqrt{205}}{7}$,
∴S△EFQ=$\frac{1}{2}$EQ•EF=$\frac{1}{2}$×$\frac{\sqrt{205}}{7}$×$\frac{3\sqrt{205}}{7}$=$\frac{615}{98}$,
在△ADE和△BME中,
$\left\{\begin{array}{l}{∠AED=∠MEB}\\{∠EAD=∠EBM}\\{ME=ED}\end{array}\right.$,
∴△ADE≌△BME(AAS),
∴AE=BE,
∴tan∠ADE=$\frac{AE}{AD}$=$\frac{AE}{AB}$=$\frac{1}{2}$,
∴tan∠EDF=$\frac{EF}{ED}$=$\frac{1}{2}$,
∴EM=ED=$\frac{6\sqrt{205}}{7}$,
∴DQ=$\frac{5\sqrt{205}}{7}$,MQ=$\frac{6\sqrt{205}}{7}$+$\frac{\sqrt{205}}{7}$=$\sqrt{205}$,
∴$\frac{DQ}{MQ}$=$\frac{\frac{5\sqrt{205}}{7}}{\sqrt{205}}$=$\frac{5}{7}$,
∴$\frac{PQ}{QF}$=$\frac{DQ}{MQ}$=$\frac{5}{7}$,
∴S△PEQ:S△FEQ=5:7,
∴S△PEQ:$\frac{615}{98}$=5:7,
∴S△PEQ=$\frac{3075}{686}$.
点评 此题考查了四边形的综合,用到的知识点是全等三角形的判定与性质、正方形的性质、特殊角的三角函数值、三角形的面积公式、相似三角形的判定与性质等,关键是根据题意作出辅助线,构造直角三角形.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{6\sqrt{3}-9}{4}$ | B. | 1+2$\sqrt{3}$ | C. | $\frac{3-\sqrt{3}}{2}$ | D. | $\frac{3}{2}$+$\frac{3}{2}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
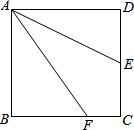 如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=$\frac{1}{2}$厘米.
如图,已知正方形ABCD的边长是2厘米,E是CD边的中点,F在BC边上移动,当AE恰好平分∠FAD时,CF=$\frac{1}{2}$厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
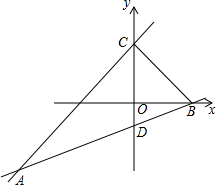 已知直线l1的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,直线l2的解析式为y=$\frac{7}{6}$x+$\frac{3}{2}$,两直线相交于点A.l1与x轴相交于点B,与y轴相交于点D,l2与y轴相交于的C.
已知直线l1的解析式为y=$\frac{1}{2}$x-$\frac{1}{2}$,直线l2的解析式为y=$\frac{7}{6}$x+$\frac{3}{2}$,两直线相交于点A.l1与x轴相交于点B,与y轴相交于点D,l2与y轴相交于的C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com