练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列几何体的主视图与其他三个不同的是（　　）

    　

    A．

    B．

    C．

    D．

    　

    　


    C   　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


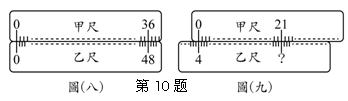
    已知甲、乙为两把不同刻度的直尺，且同一把直尺的刻度之间距离相等，小洋同学将此两把直尺紧贴，并将两直尺上的刻度0彼此对准后，发现甲尺的刻度36会对准乙尺的刻度48，如图所示。若今将甲尺向右平移且平移过程中两把直尺维持紧贴，使得甲尺的刻度0会对准乙尺的刻度4，如图(九)所示，则此时甲尺的刻度21会对准乙尺的哪一个刻度？（  ）.

    (A) 24   (B) 28   (C) 31   (D) 32

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


        问题提出

    如图①，已知直线l与线段AB平行，试只用直尺作出AB的中点．

    初步探索

    如图②，在直线l的上方取一个点E，连接EA、EB，分别与l交于点M、N，连接MB、NA，交于点D，再连接ED并延长交AB于点C，则C就是线段AB 的中点．

    推理验证

    利用图形相似的知识，我们可以推理验证AC＝CB．

    （1）若线段a、b、c、d长度均不为0，则由下列比例式中，一定可以得出b＝d的是（）

    A． ＝

    B．＝

    C．＝

    D．＝

    （2）由MN∥AB，可以推出△EFN∽△ECB，△EMN∽△EAB，△MND∽△BAD，

    △FND∽△CAD．

         所以，有＝＝＝＝，

             所以，AC＝CB．

    拓展研究

    如图③，△ABC中，D是BC的中点，点P在AB上．

    （3）在图③中只用直尺作直线l∥BC．

    （4）求证：l∥BC．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠ABC= 90°，以AB为直径的⊙O与AC边交与点D．过D作⊙O的切线交BC与点E．连接OE.   

        (1)证明：OE∥AC；

        (2)①当∠BAC=     °时，四边形ODEB是正方形；

      ②当∠BAC=     °时，AD=3DE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在0，﹣2，5，，﹣0.3中，负数的个数是（　　）

    　

    A．

    1

    B．

    2

    C．

    3

    D．

    4

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，四边形ABCD中，∠C=50°，∠B=∠D=90°，E、F分别是BC、DC上的点，当△AEF的周长最小时，∠EAF的度数为（　　）

    　

    A．

    50°

    B．

    60°

    C．

    70°

    D．

    80°

    　

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在圆心角为90°的扇形OAB中，半径OA=2cm，C为的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为　　　　　　cm2．

    　

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3，表示的点在数轴上表示时，所在哪两个字母之间（　　）

    A．C与D      B．A与B      C．A与C      D．B与C

    查看答案和解析>>

    科目：初中数学 来源： 题型：


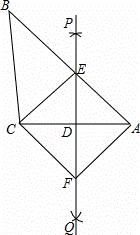
    如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．

    （1）求证：△AED≌△CFD；

    （2）求证：四边形AECF是菱形．

    （3）若AD=3，AE=5，则菱形AECF的面积是多少？

    　

    查看答案和解析>>

    同步练习册答案