
【题目】解方程
(1) 3x-2(x-1)= 2- 3(5-2x)
(2)![]()
(3)![]()
(4) ![]()
【答案】(1)x=3;(2)x=5;(3)x=-8;(4)x=-9.2
【解析】
(1)去括号,移项,合并同类项,系数化为1可得;(2)去分母,去括号,移项,合并同类项,系数化为1可得;(3)去括号,移项,合并同类项,系数化为1可得;(4)去分母,去括号,移项,合并同类项,系数化为1可得;
解:(1) 3x-2(x-1)= 2- 3(5-2x)
3x-2x+2=2-15+6x
3x-2x-6x=2-15-2
-5x=-15
x=3
(2)![]()
4(x+1)=5(x+1)-6
4x+4=5x+5-6
4x-5x=5-6-4
-x=-5
x=5
(3)![]()
![]()
![]()
![]()
![]()
x=-8
(4) ![]()
2(x-3)-5(x+4)=1.6
2x-6-5x-20=1.6
2x-5x=1.6+6+20
-3x=27.6
x=-9.2


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买A、B两种型号电脑。已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元,且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同.
(1)求A、B两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,则最多可购买A种型号电脑多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
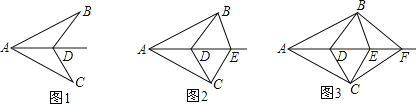
【题目】已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、BE、CE、BF、CF,图中有6对全等三角形;依此规律,第n个图形中有_____对全等三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() 、
、![]() 相交于点
相交于点![]() .(1)若
.(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到
的外接圆的圆心也随之运动,求该圆心到![]() 边的距离的最大值.
边的距离的最大值.
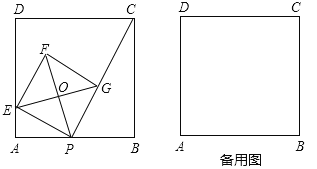
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+![]() ∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-![]() ∠A.上述说法正确的个数是( )
∠A.上述说法正确的个数是( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
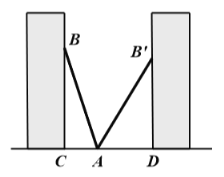
【题目】如图,小巷左右两侧是竖直的墙,一架梯子![]() 斜靠在左墙时,梯子底端到左墙角的距离
斜靠在左墙时,梯子底端到左墙角的距离![]() 为0.7米,顶端到地面距离
为0.7米,顶端到地面距离![]() 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离
为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离![]() 为2米,求小巷的宽度
为2米,求小巷的宽度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
姓 名 | 1 | 2 | 3 | 4 | 5 |
小 王 | 60 | 75 | 100 | 90 | 75 |
小 李 | 70 | 90 | 80 | 80 | 80 |
根据上表解答下列问题:
(1)完成下表:
姓 名 | 平均成绩(分) | 中位数(分) | 众数(分) | 方差 |
小 王 | 75 | 190 | ||
小 李 | 80 | 80 |
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com