
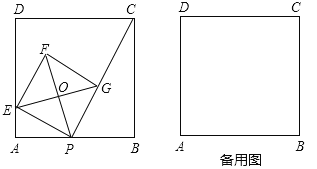
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() 、
、![]() 相交于点
相交于点![]() .(1)若
.(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到
的外接圆的圆心也随之运动,求该圆心到![]() 边的距离的最大值.
边的距离的最大值.
【答案】(1)![]() ;(2)①见解析;②2
;(2)①见解析;②2![]() ;(3)
;(3)![]() .
.
【解析】(1)根据正方形的性质得到∠A=∠B=∠EPG=90°,PF⊥EG,然后根据垂直的性质和直角三角形的两锐角互余的性质得到∠AEP=∠BPC,再根据两角对应相等的两三角形相似证得△APE∽△BCP,最后根据相似三角形的对应边成比例求解即可;
(2)①证明A、P、O、E四点共圆,即可得出结论;
②连接OA、AC,由勾股定理得到AC的长,由圆周角定理得出∠OAP=∠OEP=45°,点O在AC上,当点P运动到点B时,O为AC 的中点,即可求解;
(3)设△APE的外接圆的圆心为M,作MN⊥AB于N,由三角形中位线定理得到MN=![]() AE,设AP=x,则BP=4-x,由(1)中的相似三角形的性质:对应边成比例,求出AE= x-
AE,设AP=x,则BP=4-x,由(1)中的相似三角形的性质:对应边成比例,求出AE= x-![]() x2=-
x2=-![]() (x-2)2+1,由二次函数的最值求出AE的最大值为1,然后可求MN的值.
(x-2)2+1,由二次函数的最值求出AE的最大值为1,然后可求MN的值.
(1)解:∵四边形ABCD、四边形PEFG是正方形,
∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,
∴∠AEP+∠APE=90°,∠BPC+∠APE=90°,
∴∠AEP=∠BPC,
∴△APE∽△BCP,
∴![]() ,即
,即![]() ,
,
解得:AE=![]() ;
;
(2)①证明:∵PF⊥EG,
∴∠EOP=90°,
∴∠EOP+∠A=180°,
∴A、P、O、E四点共圆,
∴点O一定在△APE的外接圆上;
②解:连接OA、AC,如图1所示:
∵四边形ABCD是正方形,
∴∠B=90°,∠BAC=45°,
∴AC=![]() ,
,
∵A、P、O、E四点共圆,
∴∠OAP=∠OEP=45°,
∴点O在AC上,
当P运动到点B时,O为AC的中点,OA=![]() AC=2
AC=2![]() ,
,
即点O经过的路径长为2![]() ;
;
(3)解:设△APE的外接圆的圆心为M,作MN⊥AB于N,如图2所示:
则MN∥AE,
∵ME=MP,
∴AN=PN,
∴MN=![]() AE,
AE,
设AP=x,则BP=4-x,
由(1)得:△APE∽△BCP,
∴![]() ,即
,即![]() ,
,
解得:AE=x-![]() x2=-
x2=-![]() (x-2)2+1,
(x-2)2+1,
∴x=2时,AE的最大值为1,此时MN的值最大=![]() ×1=
×1=![]() ,即△APE的圆心到AB边的距离的最大值为
,即△APE的圆心到AB边的距离的最大值为![]() .
.


科目:初中数学 来源: 题型:
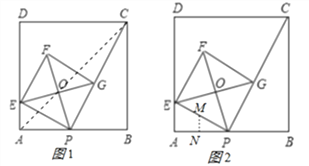
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (a≠0)的图像与x轴交于点A(-2,0)、B,与y轴交于点C,tan∠ABC=2.
(a≠0)的图像与x轴交于点A(-2,0)、B,与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
(3)在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以2cm/s和3cm/s的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为( )
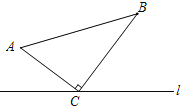
A. 4.6或7B. 7或8C. 4.6或8D. 4.6或7或8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知 AD 是△ABC 的边 BC 上的中线.
(1)作出△ABD 的边 BD 上的高.
(2)若△ABC 的面积为 10,求△ADC 的面积.
(3)若△ABD 的面积为 6,且 BD 边上的高为 3,求 BC 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明学校门前有座山,山上有一电线杆PQ,他很想知道电线杆PQ 的高度.于是,有一天,小明和他的同学小亮带着侧倾器和皮尺来到山脚下进行测量.测量方案如下:如图,首先,小明站在地面上的点A处,测得电线杆顶端点P的仰角是45![]() ;然后小明向前走6米到达点B处,测得电线杆顶端点P和电线杆底端点Q的仰角分别是60
;然后小明向前走6米到达点B处,测得电线杆顶端点P和电线杆底端点Q的仰角分别是60![]() 和30
和30![]() ,设小明的眼睛到地面的距离为1.6米.请根据以上测量的数据,计算电线杆PQ的高度(结果精确到1米)参考数据:
,设小明的眼睛到地面的距离为1.6米.请根据以上测量的数据,计算电线杆PQ的高度(结果精确到1米)参考数据:![]() .
.
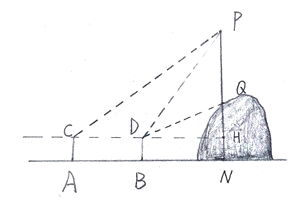
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王先生到泉州台商投资区行政服务中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作﹣1,王先生从1楼出发,电梯上下楼层依次记录如下:(单位:层)
+6,﹣3,+10,﹣8,+12,﹣7,﹣10.
(1)请你通过计算说明王先生最后是否回到出发点1楼.
(2)该中心大楼每层高3m,电梯每向上或下1m需要耗电0.1度,根据王先生现在所处位置,请你算算,他办事时电梯需要耗电多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com