
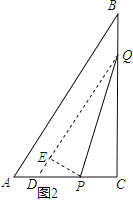
����Ŀ����ͼ1����Rt��ABC�У���ACB=90����AC=6cm��BC=8cm����P��A������AC��C����1����/����ٶ������ƶ�����Q��C������CB��B����2����/����ٶ������ƶ�����P��Q�ֱ�����ͬʱ�������ƶ���ijһλ��ʱ����ʱ��Ϊt�룮

��1����t=2ʱ�����߶�PQ�ij��ȣ�
��2����tΪ��ֵʱ����PCQ���������5cm2��
��3����P��Q�˶������У���ijһʱ�̣�������PQC���ۣ��õ���EPQ����ͼ2��PE��AB�ܷ�ֱ�����ܣ������Ӧ��tֵ�������ܣ���˵�����ɣ�
���𰸡���1��![]() ���ף���2����t=1��ʱ����PCQ���������5cm2����3����t=
���ף���2����t=1��ʱ����PCQ���������5cm2����3����t=![]() ʱ��PE��AB��
ʱ��PE��AB��
��������
�����������1����t=2ʱ�������CP��CQ�ij������ݹ��ɶ�����������߶μ�б��PQ�ij���
��2���������������ʽ�ɽ�������t�ķ��̣��ⷽ�����t��ֵ���ɣ�
��3���ӳ�QE��AC�ڵ�D����PE��AB����QD��AB�����Կɵ���CQD�ס�CBA�������������ε����ʣ���Ӧ�ߵı�ֵ��ȿ����DE=0.5t����֤��ABC�ס�DPE���������������ε����ʿɵ�![]() ������֪���ݴ��뼴�����t��ֵ��
������֪���ݴ��뼴�����t��ֵ��
�⣺��1����t=2ʱ��
����P��A������AC��C����1����/����ٶ������ƶ�����Q��C������CB��B����2����/����ٶ������ƶ���
��AP=2���ף�QC=4���ף�
��PC=4����Rt��PQC��PQ=![]() =
=![]() ���ף�
���ף�
��2������P��A������AC��C����1����/����ٶ������ƶ�����Q��C������CB��B����2����/����ٶ������ƶ���
��PC=AC��AP=6��t��CQ=2t��
��S��CPQ=![]() CPCQ=
CPCQ=![]() ��
��
��t2��6t+5=0
���t1=1��t2=5���������⣬��ȥ��
����t=1��ʱ����PCQ���������5cm2��
��3���ܴ�ֱ���������£�
�ӳ�QE��AC�ڵ�D��
������PQC���ۣ��õ���EPQ��
���QCP�ա�QEP��
���C=��QEP=90����
��PE��AB����QD��AB��
���CQD�ס�CBA��
��![]() ��
��
��![]() ��
��
��QD=2.5t��
��QC=QE=2t
��DE=0.5t
��֤��ABC�ס�DPE��
��![]()
��![]() ��
��
��ã�t=![]() ��0��t��4����
��0��t��4����
���Ͽ�֪����t=![]() ʱ��PE��AB��
ʱ��PE��AB��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
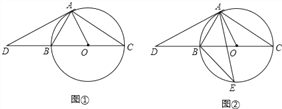
����Ŀ����֪BC����O��ֱ����AD����O�����ߣ��е�ΪA��AD��CB���ӳ����ڵ�D������AB��AO��
��1����ͼ������֤����OAC=��DAB��
��2����ͼ�ڣ�AD=AC����E����O��һ�㣬����E�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�C˳ʱ����ת90��õ���EDC������A��D��E��ͬһ��ֱ���ϣ���ACB=20�㣬���ADC�Ķ�����![]() ����
����![]()

A. 55�� B. 60�� C. 65�� D. 70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ��
��![]() ���ڽ������Σ�
���ڽ������Σ�![]() ��
��![]() �ӳ����ϵ�һ�㣬����
�ӳ����ϵ�һ�㣬����![]() ����
����![]() .
.
��1���ж�ֱ��![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��2����![]() ��
��![]() ������
������![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����Լƻ�ֲ�����Ͱ����������г�������Ԥ�⣬��ֲ����������![]() ����Ԫ����Ͷ�ʳɱ�x����Ԫ��������ͼ����ʾ�Ķ��κ���
����Ԫ����Ͷ�ʳɱ�x����Ԫ��������ͼ����ʾ�Ķ��κ���![]() ����ֲ����������
����ֲ����������![]() ����Ԫ����Ͷ�ʳɱ�x����Ԫ��������ͼ����ʾ������������
����Ԫ����Ͷ�ʳɱ�x����Ԫ��������ͼ����ʾ������������![]() =kx��
=kx��
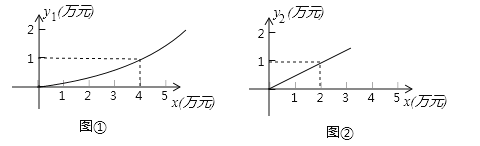
��1���ֱ��������![]() ����Ԫ��������
����Ԫ��������![]() ����Ԫ������Ͷ�ʳɱ�x����Ԫ���ĺ�����ϵʽ��
����Ԫ������Ͷ�ʳɱ�x����Ԫ���ĺ�����ϵʽ��
��2��������������10��Ԫ�ʽ�Ͷ����ֲ�����Ͱ�����������Ͷ�ʳɱ�������2��Ԫ�Ҳ�����8��Ԫ���������ٻ�ö�����������ܻ�ö�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ���ĸ�С�������Ϸֱ�������֩�2��0��1��2�����dz����ֲ�ͬ��û���κ�����ÿ��ʵ���Ƚ�����ȣ�
��1��������ȡһ�����ȡ������Ϊ�����ĸ��ʣ�
��2��������ȡһ�����ϵ����ּ�Ϊx�����Żأ�������ȡһ�����ϵ����ּ�Ϊy�����û���״ͼ�����б�������ʾ���п��ܳ��ֵĽ��������x+y��0���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ��� y��ax+bx+c��a��0����ͼ����ͼ��ʾ��A���� 1��3���������ߵĶ��㣬�����½�������ȷ���ǣ� ��
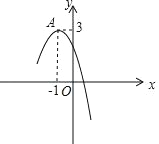
A. a��0��b��0��c��0
B. 2a+b��0
C. �� x��0 ʱ��y �� x ���������С
D. ax2+bx+c��3��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ΪԤ��������ijУ�Խ��ҽ�����ҩѬ����������֪ҩ��ȼ�սΣ�����ÿ���������еĺ�ҩ��![]() ��mg����ȼ��ʱ��
��mg����ȼ��ʱ��![]() �����ӣ�����������ȼ�պ�
�����ӣ�����������ȼ�պ� ![]() ��
��![]() �ɷ���������ͼ��ʾ�����ֲ��ҩ��10����ȼ�꣬��ʱ������ÿ����������ҩ��Ϊ8mg����������Ϣ����������⣺
�ɷ���������ͼ��ʾ�����ֲ��ҩ��10����ȼ�꣬��ʱ������ÿ����������ҩ��Ϊ8mg����������Ϣ����������⣺
��1����ҩ��ȼ��ʱ![]() ��
��![]() �ĺ�����ϵʽ����2����ҩ��ȼ�պ�
�ĺ�����ϵʽ����2����ҩ��ȼ�պ�![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3����ÿ���������к�ҩ������1.6mgʱ�������巽���������ã���ô��������ʼ�����ʱ��ѧ���ſ��Իؽ��ң�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
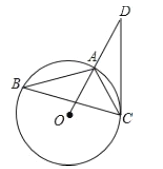
����Ŀ����ͼ��ACΪ��O��ֱ����BΪ��O��һ�㣬��ACB=30�㣬�ӳ�CB����D��ʹ��CB=BD������D��DE��AC������E��CA���ӳ����ϣ�����BE��
��1����֤��BE����O�����ߣ�
��2����BE=3ʱ����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com