
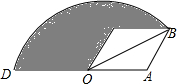
 如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$.
如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$. 分析 首先过点B作BE⊥AD于点E,由在菱形OABC中,∠C=120°,OA=2,可求得BE与OB的长,∠BOD的度数,然后由S阴影=S扇形OBD-S△BOC求得答案.
解答 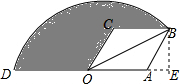 解:过点B作BE⊥AD于点E,
解:过点B作BE⊥AD于点E,
∵在菱形OABC中,∠C=120°,OA=2,
∴∠AOC=180°-∠C=60°,∠OAB=∠C=120°,AB=OA=2,
∴∠AOB=$\frac{1}{2}$∠AOC=30°,∠BAE=180°-∠BAO=60°,
∴BE=AB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,∠BOD=180°-∠AOB=150°,
∴OB=2BE=2$\sqrt{3}$,
∴S△OBC=S△AOB=$\frac{1}{2}$OA•BE=$\sqrt{3}$,S扇形OBD=$\frac{150×π×(2\sqrt{3})^{2}}{360}$=5π,
∴S阴影=S扇形OBD-S△BOC=5π-$\sqrt{3}$.
故答案为:5π-$\sqrt{3}$.
点评 此题考查了菱形的性质、扇形的面积公式以及含30°的直角三角形的性质.注意求得△OBC与扇形OBD的面积是关键.


科目:初中数学 来源: 题型:解答题
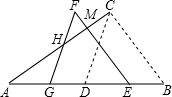 如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.
如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
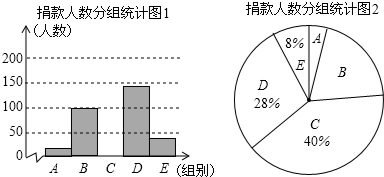
| 组别 | 捐款额x/元 | 人数 |
| A | 1≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | 200 |
| D | 30≤x<40 | 140 |
| E | 40≤x | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 27,26 | B. | 27,26.5 | C. | 26.5,27 | D. | 26,27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
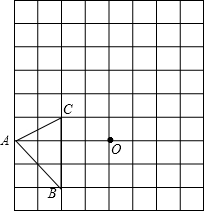 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:
如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com