
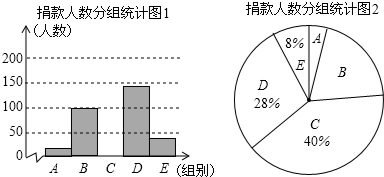
| 组别 | 捐款额x/元 | 人数 |
| A | 1≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | 200 |
| D | 30≤x<40 | 140 |
| E | 40≤x | 40 |
分析 (1)根据a与100的比值是1:5,即可求得a的值,然后根据百分比的意义求得样本容量;
(2)根据百分比的意义求得C类的人数,即可补全统计图;根据B类人数占调查人数比例乘以周角可得圆心角度数;
(3)利用总人数2200乘以对应的百分比即可
解答 解:(1)依题意有a:100=1:5,
解得:a=20,
调查的样本容量是:(20+100)÷(1-8%-28%-40%)=500.
(2)C类的人数是:500×40%=200(人).
扇形B的圆心角度数为:$\frac{100}{500}$×360°=72°;
(3)捐数值不少于30元的学生人数是:2200×(28%+8%)=792(人).
答:捐数值不少于30元的学生约有792人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
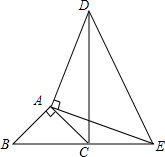 已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上.
已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
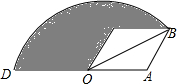 如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$.
如图,在菱形OABC中,∠C=120°,OA=2,以点O为圆心,OB的长为半径画弧,交OA的延长线于点D,则图中阴影部分的面积为5π-$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
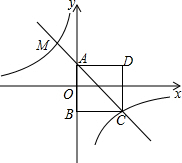 如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
如图,四边形ABCD为正方形,点A的坐标为(0,1),点B的坐标为(0,-2),反比例函数y=$\frac{k}{x}$的图象经过点C,一次函数y=ax+b的图象经过A、C两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com