
分析 (1)运用平方差公式分解,再去括号展开,最后合并同类二次根式即可;
(2)先化简各二次根式,再合并同类二次根式即可.
解答 解:(1)原式=($\sqrt{3}$-1+2$\sqrt{3}$)×($\sqrt{3}-1-2\sqrt{3}$)
=(3$\sqrt{3}$-1)×(-1-$\sqrt{3}$)
=-3$\sqrt{3}$-9+1+$\sqrt{3}$
=-2$\sqrt{3}$-8;
(2)原式=4$\sqrt{2}$-$\frac{5\sqrt{2}}{2}$+$\frac{3\sqrt{2}}{2}$
=4$\sqrt{2}$-$\sqrt{2}$
=3$\sqrt{2}$.
点评 本题主要考查二次根式的混合运算,熟练掌握二次根式混合运算的顺序和二次根式的相关性质是解题的关键.


科目:初中数学 来源: 题型:解答题
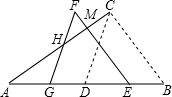 如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.
如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
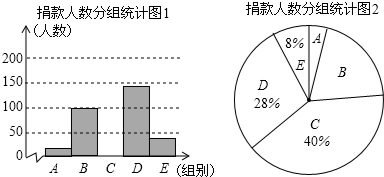
| 组别 | 捐款额x/元 | 人数 |
| A | 1≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | 200 |
| D | 30≤x<40 | 140 |
| E | 40≤x | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
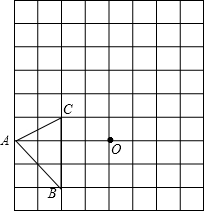 如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:
如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
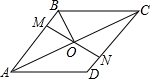 如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )
如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC的度数为( )| A. | 28° | B. | 52° | C. | 62° | D. | 72° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com