
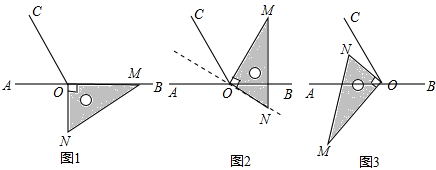
分析 (1)周角减去∠BOC、∠MON即可求解;
(2)由角的平分线的定义和等角的余角相等求解;
(3)由∠MON=90°,∠AOC=60°,可知∠AOM=90°-∠AON、∠NOC=60°-∠AON,最后求得两角的差,从而可作出判断.
解答 解:(1)∵∠BOC=120°,∠MON=90°,
∴∠NOC=360°-∠BOC-∠MON=150°;
(2)是,
如图,设ON的反向延长线为OD,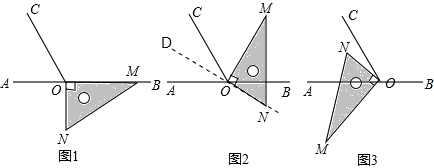
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON,
∴∠COD=∠AOD,
∴OD平分∠AOC
即直线ON平分∠AOC;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON、∠NOC=60°-∠AON.
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.
点评 此题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:解答题
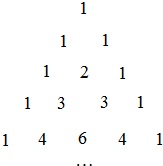 如图为杨辉三角表,它可以帮助我们按某种规律写出(a+b)n(n为自然数)展开式的系数,如:
如图为杨辉三角表,它可以帮助我们按某种规律写出(a+b)n(n为自然数)展开式的系数,如:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
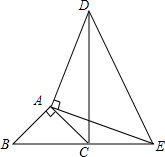 已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上.
已知,等腰△ABC和等腰△ADE以A点为公共顶点如图放置,∠BAC=∠DAE=Rt∠,B、C、E三点在同一直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com