
【题目】如图,已知C为线段AB上的一点,△ACM和△CBN都是等边三角形,AN和CM相交于F点,BM和CN交于E点.求证:△CEF是等边三角形.
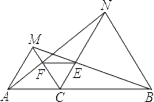
【答案】见解析
【解析】
由等边三角形的性质可得AC=CM,BC=CN,再利用角的和差可得到∠ACN=∠MCB,可证明△ACN≌△MCB,可得∠ENC=∠FBC,由条件可得∠ECF=60°,可证明△CEN≌△CFB,可得CE=CF,可知△CEF为等边三角形.
证明:∵△ACM和△CBN是等边三角形,
∴AC=MC,BC=CN,∠MCA=∠NCB=60°,
∴∠ACN=∠MCB=120°,
在△ACN和△MCB中,
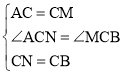 ,
,
∴△ACN≌△MCB(SAS),
∴∠ANC=∠MBC,
∵△ACM和△CBN是等边三角形,
∴∠MCA=∠NCB=60°,
∴∠ECF=180°﹣60°﹣60°=60°,
在△CFN和△CEB中,
 ,
,
∴△CFN≌△CEB(ASA),
∴CE=CF,
∵∠ECF=60°,
∴△CEF为等边三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将命题“在同圆中,相等的圆心角所对的弧相等,所对的弦也相等”改写成“已知……求证……”的形式,下列正确的是( )
A.已知:在⊙O中,∠AOB=∠COD,弧AB=弧CD.求证:AB=CD
B.已知:在⊙O中,∠AOB=∠COD,弧AB=弧BC.求证:AD=BC
C.已知:在⊙O中,∠AOB=∠COD.求证:弧AD=弧BC,AD=BC
D.已知:在⊙O中,∠AOB=∠COD.求证:弧AB=弧CD,AB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
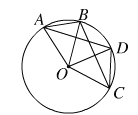
【题目】如图,已知反比例函数![]() 和一次函数
和一次函数![]() 的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
的图象相交于第一象限内的点A,且点A的横坐标为1.过点A作AB⊥x轴于点B,△AOB的面积为1.
(1)求反比例函数和一次函数的解析式.
(2)若一次函数![]() 的图象与x轴相交于点C,求∠ACO的度数.
的图象与x轴相交于点C,求∠ACO的度数.
(3)结合图象直接写出:当![]() >
>![]() >0时,x的取值范围.
>0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+4x+c(a≠0)与反比例函数y=![]() 的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
的图象相交于点B,且点B的横坐标为5,抛物线与y轴交于点C(0,6),A是抛物线的顶点,P和Q分别是x轴和y轴上的两个动点,则AQ+QP+PB的最小值为_____.
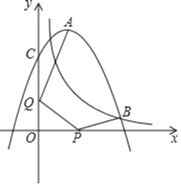
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一次函数y=mx+n和二次函数y=mx2+nx+1,其中m≠0,
(1)若二次函数y=mx2+nx+1经过点(2,0),(3,1),试分别求出两个函数的解析式.
(2)若一次函数y=mx+n经过点(2,0),且图象经过第一、三象限.二次函数y=mx2+nx+1经过点(a,y1)和(a+1,y2),且y1>y2,请求出a的取值范围.
(3)若二次函数y=mx2+nx+1的顶点坐标为A(h,k)(h≠0),同时二次函数y=x2+x+1也经过A点,已知﹣1<h<1,请求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一台灯放置在水平桌面上,底座AB与桌面垂直,底座高AB=5cm,连杆BC=CD=20cm,BC,CD与AB始终在同一平面内.
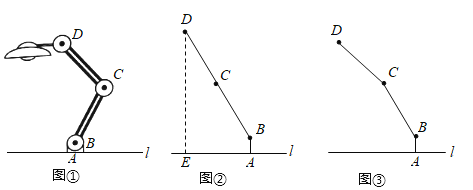
(1)如图②,转动连杆BC,CD,使∠BCD成平角,∠ABC=143°,求连杆端点D离桌面l的高度DE.
(2)将图②中的连杆CD再绕点C逆时针旋转16°,如图③,此时连杆端点D离桌面l的高度减小了 cm.
(参考数据:sin37°=0.6,cos37°=0.8,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在玩转盘游戏时,把两个可以自由转动的转盘A、B分成4等份、3等份的扇形区域,并在每一小区域内标上数字(如图所示),指针的位置固定.游戏规则:同时转动两个转盘,当转盘停止后,若指针所指两个区域的数字之和为3的倍数,甲胜;若指针所指两个区域的数字之和为4的倍数时,乙胜.如果指针落在分割线上,则需要重新转动转盘.

(1)试用列表或画树形图的方法,求甲获胜的概率;
(2)请问这个游戏规则对甲、乙双方公平吗?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发沿AB方向向终点B匀速移动,速度为1cm/s,点Q由点B出发沿BC方向向终点C匀速移动,速度为2cm/s.如果动点P,Q同时从A,B出发,当P或Q到达终点时运动停止.几秒后,以Q,B,P为顶点的三角形与△ABC相似?
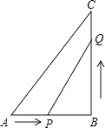
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,园林小组的同学用一段长16米的篱笆围成一个一边靠墙的矩形菜园ABCD,墙的长度为9米,设AB的长为x米,BC的长为y米.
(1)①写出y与x的函数关系是: ;
②自变量x的取值范围是 ;
(2)园林小组的同学计划使矩形菜园的面积为30平方米,试求此时边AB的长.
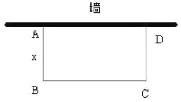
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com