
分析 首先确定中心角为60°的正多边形的边数,然后利用其边长求其外接圆的半径求出边长,由勾股定理求出内切圆半径即可.
解答 解:这个正多边形的边数:360°÷60°=6.
正六边形的半径与边长相等,
∴正六边形的边长=2,
如图所示:O为外接圆的圆心,
作OM⊥AB于M,连接OA,
则AM=$\frac{1}{2}$AB=1,
∴OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
即正六边形的内切圆半径为$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 考查了正多边形和圆的知识、勾股定理;正六边形的半径与边长相等,是需要熟记的内容.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AC=1,BC=2,AB=$\sqrt{5}$,则cosB的值是( )
如图,在△ABC中,AC=1,BC=2,AB=$\sqrt{5}$,则cosB的值是( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为$\frac{1+\sqrt{5}}{2}$.
如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 甲种材料(千克) | 乙种材料(千克) |
| 1件A产品所需材料 | 4 | 1 |
| 1件B产品所需材料 | 3 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
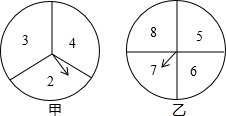 如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
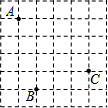 如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )| A. | (2,-3) | B. | (1,1) | C. | (-1,1) | D. | (1,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com