
����Ŀ����ͼ��ʾ��ֱ��AC��BD������AB��ֱ��AC��BD���߶�AB��ƽ��ֳɢ١��ڡ��ۡ����ĸ����֣��涨�����ϸ��㲻�����κβ��֣�������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ���ʾ���й����˵�������غϵ���������ɵĽ���0�㣩��
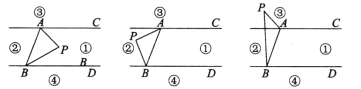
��1��������P���ڵڢٲ���ʱ����֤����APB����PAC����PBD��
��2��������P���ڵڢڲ���ʱ����APB����PAC����PBD�Ƿ������ֱ�ӻش������������
��3��������P�ڵڢ۲���ʱ��ȫ��̽����PAC����APB����PBD֮��Ĺ�ϵ����д������P�ľ���λ�ú���Ӧ�Ľ��ۣ�ѡ������һ�ֽ��ۼ���֤����
���𰸡���1��֤������������2������������3��֤��������
��������
��1����ͼ���ӳ�BP��ֱ��AC�ڵ�E����AC��BD����֪��PEA=��PBD���ɡ�APB=��PAE+��PEA����֪��APB=��PAC+��PBD��
��2������P��AC��ƽ���ߣ�����ƽ���ߵ����ʽ��
��3������P�IJ�ͬλ�ã��֢ٵ�����P������BA���Ҳ�ʱ���ڵ�����P������BA��ʱ���۵�����P������BA�����ʱ������������ۣ�
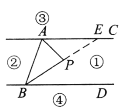
�⣺��1����ͼ��ʾ���ӳ�BP��ֱ��AC�ڵ�E��
��ΪAC��BD�����ԡ�PEA����PBD��
��Ϊ��APB����PAE+��PEA�����ԡ�APB����PAC+��PBD��
��2���������� ��
��P��PM��AC��
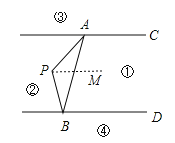
��AC��BD��
��AC��PM��BD��
���PAC+��APM=180������PBD+��BPM=180����
���APB+��PAC+��PBD=360�����������Ƴ���APB=��PAC+��PBD��
�ʲ�������
��3���ٵ�����P������BA���Ҳ�ʱ�������ǡ�PBD=��PAC+��APB��
�ڵ�����P������BA��ʱ�������ǡ�PBD����PAC+��APB�����PAC����PBD+��APB���APB��0�㣬��PAC=��PBD����дһ�����ɣ���
�۵�����P������BA�����ʱ�������ǡ�PAC=��APB+��PBD
ѡ���֤����
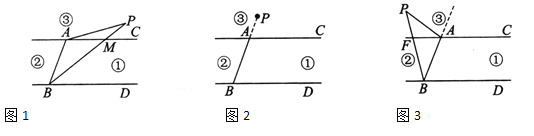
��ͼ1��ʾ������PA������PB��AC�ڵ�M��
��ΪAC��BD�����ԡ�PMC����PBD��
����Ϊ��PMC����PAMʮ��APM�����ԡ�PBD����PAC+��APB��
ѡ���֤������ͼ2��ʾ����Ϊ��P������BA�ϣ����ԡ�APB��0�㣮
��ΪAC��BD�����ԡ�PBD����PAC��
���ԡ�PBD����PAC����APB���PAC=��PBD+��APB���APB��0�㣬��PAC=��PBD��
ѡ���֤�������ͼ3��ʾ������PA������PB��AC�ڵ�F��
��ΪAC��BD�����ԡ�PFA����PBD��
��Ϊ��PAC����APF+��PFA�����ԡ�PAC����APF+��PBD��
���ԡ�PAC=��APB+��PBD��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��AD=4����P�ӵ�A������������AC��CB���յ�B�˶�����P��AC�ϵ��ٶ�Ϊÿ��2����λ���ȣ���CB�ϵ��ٶ�Ϊÿ��1����λ���ȣ�ͬʱ����Q�ӵ�A��������AC��ÿ��1����λ���ȵ��ٶ����յ�C�˶�������Q�����յ�ʱ����PҲ��ֹ֮ͣ������P��PM��AD�ڵ�M������QM����PM��QMΪ�ڱ���PMQN����PMQN�����ABCD�ص�����ͼ�ε��ܳ�Ϊd�����ȵ�λ������P���˶�ʱ��Ϊt���룩��t��0��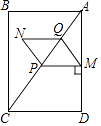
��1����AC�ij�
��2���ú�t�Ĵ���ʽ��ʾ�߶�CP�ij���
��3������P���߶�AC��ʱ����d��t֮��ĺ�����ϵʽ��
��4��������N��ֱ�߽�����ABCD�����ƽ�֣�����ֱ��ͬʱ��PMQN������ֳ�1��3�������֣�ֱ��д����ʱt��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���ABCD��AC��BD�ཻ�ڵ�O��AB=4��AC=6��BD=10����1�����ACD�Ķ�������2����BC�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
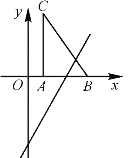
����Ŀ����ͼ����Rt��ABC����ƽ��ֱ������ϵ�ڣ����С�CAB��90����BC��5����A��B������ֱ�Ϊ(1��0)��(4��0)������ABC��![]() ������ƽ�ƣ�����C����ֱ��
������ƽ�ƣ�����C����ֱ��![]() ��ʱ���߶�BCɨ�������Ϊ( )
��ʱ���߶�BCɨ�������Ϊ( )
A. 16B. 8C. 8![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪A��B��������y=ax2��a��0����������ͬ�ĵ㣬����A�ڵڶ����ޣ�B�ڵ�һ���ޣ�
��1����ͼ1��ʾ����ֱ��AB��x��ƽ�У���AOB=90�㣬��AB=2ʱ����������ߵĽ���ʽ��A��B����ĺ�����ij˻���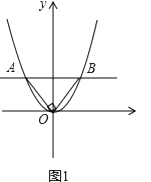
��2����ͼ2��ʾ���ڣ�1������õ��������ϣ���ֱ��AB��x�ƽ�У���AOB��Ϊ90��ʱ����֤��A��B���������ij˻���һ����ֵ��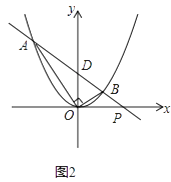
��3���ڣ�2���������£����ֱ��AB��x�ᡢy��ֱ��ڵ�P��D���ҵ�B�ĺ�����Ϊ ![]() ����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ռ����������ݣ�
ij��ѧ�ߣ�1����ѧϰ��ͳ��֪ʶ����ѧ��ʦҪ��ÿ��ѧ���ͱ���ѧ������ѧ��ʽ����һ��ȫ����飬��ͼ��һͬѧͨ���ռ����ݺ���Ƶ�������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺��ÿ��ѧ��ֻѡ��1����ѧ��ʽ����

��1����ð�˳���ѧ��������
��2����Ƶ���ֲ�ֱ��ͼ����������
��3������У���꼶��1200��ѧ�����ܷ��ɴ˹��Ƴ���У���꼶ѧ�������г���ѧ��������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���Ϳ�����Ⱦ�������ɺ�����˾����ȫ���������ܻ�����ȼ�����������ƻ�����A�ͺ�B�����ֹ�������10��������ÿ̨�ļ۸����ؿ��������
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
���ؿ���������/�꣩ | 60 | 100 |
������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ��
��1����a��b��ֵ��
��2������ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ��ܺͲ�����680���˴Σ��������һ��������ʹ�ù����ܷ������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��AB��DC����PΪƽ����һ�㣬����AP��CP��
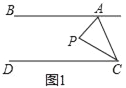
��1����ͼ1����P��ֱ��AB��CD֮�䣬����BAP=60�㣬��DCP=20��ʱ�����APC��
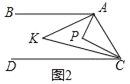
��2����ͼ2����P��ֱ��AB��CD֮�䣬��BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K��д����AKC���APC֮���������ϵ����˵�����ɣ�
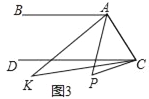
��3����ͼ3����P����CD�⣬��BAP���DCP�Ľ�ƽ�����ཻ�ڵ�K����AKC���APC�к�������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ſ�����ȵľ��ε�����һ��õ���ͼ��ʾ���ı���ABCD�����ı���ABCD��___________�Σ������ž���ֽƬ�ij�����10��������4����ô�ı���ABCD�ܳ������ֵ=___________��
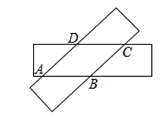
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com