
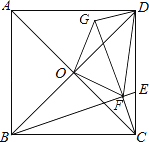
【题目】如图,正方形ABCD的边长为12,点O为对角线AC、BD的交点,点E在CD上,tan∠CBE= ![]() ,过点C作CF⊥BE,垂足为F,连接OF,将△OCF绕着点O逆时针旋转90°得到△ODG,连接FG、FD,则△DFG的面积是________.
,过点C作CF⊥BE,垂足为F,连接OF,将△OCF绕着点O逆时针旋转90°得到△ODG,连接FG、FD,则△DFG的面积是________.
【答案】![]()
【解析】
根据tan∠CBE=![]() 可得CE的长度,利用勾股定理可求出BE的长度,利用面积公式可求出CF的长度,根据正方形的性质及旋转的性质可得∠BCF=∠CGD,CF=DG,通过证明△BCF≌△CDG,可得∠FGD=90°,利用勾股定理可求出CG的长,进而可得GF的长,根据三角形面积公式即可得答案.
可得CE的长度,利用勾股定理可求出BE的长度,利用面积公式可求出CF的长度,根据正方形的性质及旋转的性质可得∠BCF=∠CGD,CF=DG,通过证明△BCF≌△CDG,可得∠FGD=90°,利用勾股定理可求出CG的长,进而可得GF的长,根据三角形面积公式即可得答案.
∵tan∠CBE=![]() ;BC=12,
;BC=12,
∴CE=12![]() tan∠CBE=4,
tan∠CBE=4,
∴BE=![]() =4
=4![]() ,
,
∵CF⊥BE,
∴![]() BC×CE=
BC×CE=![]() BE×CF,
BE×CF,
∴CF=![]() =
=![]() ,
,
∴DG=![]() ,
,
∵△OCF绕着点O逆时针旋转90°得到△ODG,
∴∠OCF=∠ODG,CF=DG
∵AC、BD是正方形ABCD的对角线,
∴∠ACB=∠BDC=45°,
∴∠ACB+∠OCF=∠BDC+∠ODG,即∠BCF=∠CDG,
又∵BC=CD,CF=DG,
∴△BCF≌△CDG,
∴∠BFC=∠CDG=90°,
∴CG=![]() =
=![]() =
=![]() ;
;
∴GF=CG-CF=![]() -
-![]() =
=![]() ,
,
∴S△DFG=![]() GF
GF![]() DG=
DG=![]()
![]()
![]() =
=![]() ,
,
故答案为:![]()


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
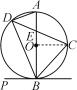
【题目】如图:C、D是以AB为直径的⊙O上的点,![]() ,弦CD交AB于点E.
,弦CD交AB于点E.
(1)当PB是⊙O的切线时,求证:∠PBD=∠DAB;
(2)求证:BC2-CE2=CE·DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以![]() 的边
的边![]() ,
,![]() 所在直线为对称轴作
所在直线为对称轴作![]() 的对称图形
的对称图形![]() 和
和![]() ,
,![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() .有如下结论:①
.有如下结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;其中正确的结论个数是( )
;其中正确的结论个数是( )
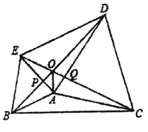
A.0个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
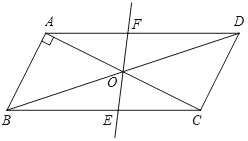
【题目】如图,在ABCD中,AB=1,BC=![]() ,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
(1)证明:当旋转角为 时,四边形ABEF是平行四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时AC绕点O顺时针旋转的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
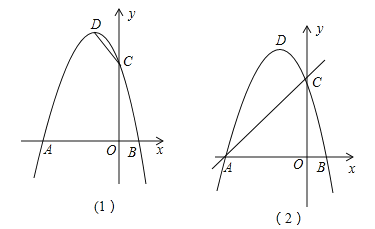
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,上午8时,一条船从![]() 处测得灯塔
处测得灯塔![]() 在北偏西
在北偏西![]() ,以15海里/时的速度向北航行,9时30分到达
,以15海里/时的速度向北航行,9时30分到达![]() 处,测得灯塔
处,测得灯塔![]() 在北偏西
在北偏西![]() ,若船继续向正北方向航行,求轮船何时到达灯塔
,若船继续向正北方向航行,求轮船何时到达灯塔![]() 的正东方向
的正东方向![]() 处.
处.
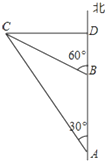
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;则其中说法正确的是( ).

A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500 m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
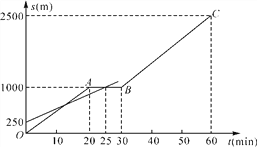
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,完成下列各题:
,完成下列各题:

![]() 将函数关系式用配方法化为
将函数关系式用配方法化为![]() 的形式,并写出它的顶点坐标、对称轴.
的形式,并写出它的顶点坐标、对称轴.
![]() 求出它的图象与坐标轴的交点坐标.
求出它的图象与坐标轴的交点坐标.
![]() 在直角坐标系中,画出它的图象.
在直角坐标系中,画出它的图象.
![]() 根据图象说明:当
根据图象说明:当![]() 为何值时,
为何值时,![]() ;当
;当![]() 为何值时,
为何值时,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com