
【题目】如图,在ABCD中,AB=1,BC=![]() ,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
,对角线AC,BD交于O点,将直线AC绕点O顺时针旋转,分别交于BC,AD于点E,F.
(1)证明:当旋转角为 时,四边形ABEF是平行四边形;
(2)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时AC绕点O顺时针旋转的度数.
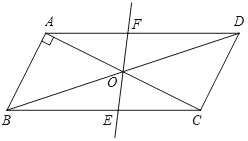
【答案】(1)90°;(2)在旋转过程中,四边形BEDF能是菱形,此时AC绕点O顺时针旋转的度数是45°.
【解析】
(1)根据∠BAC=∠AOF=90°推出AB∥EF,根据平行四边形性质得出AF∥BE,即可推出四边形ABEF是平行四边形;
(2)证△DFO≌△BEO,推出OF=OE,得出四边形BEDF是平行四边形,根据勾股定理求出AC,求出OA=AB=1,求出∠AOB=45°,根据∠AOF=45°,推出EF⊥BD,根据菱形的判定推出即可.
解:(1)结论:旋转角为90°时,四边形ABEF是平行四边形.
理由:∵∠AOF=90°,∠BAO=90°,
∴∠BAO=∠AOF,
∴AB∥EF,
又∵四边形ABCD是平行四边形,
∴AF∥EB,
∴四边形ABEF是平行四边形;
(2)当旋转角∠AOF=45°时,四边形BEDF是菱形.理由如下:

∵四边形ABCD是平行四边形,
∴AD∥BC,BO=DO,
∴∠FDO=∠EBO,∠DFO=∠BEO,
在△DFO和△BEO中
∵ ,
,
∴△DFO≌△BEO(AAS),
∴OF=OE,
∴四边形BEDF是平行四边形,
∵AB=1,BC=![]() ,
,
∴在Rt△BAC中,由勾股定理得:AC=2,
∴AO=1=AB,∵∠BAO=90°,
∴∠AOB=45°,
又∵∠AOF=45°,
∴∠BOF=90°,
∴BD⊥EF,
∴四边形BEDF是菱形,
即在旋转过程中,四边形BEDF能是菱形,此时AC绕点O顺时针旋转的度数是45°.


科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某船自西向东航行,在![]() 处测得某岛
处测得某岛![]() 在北偏东
在北偏东![]() 的方向上,前进
的方向上,前进![]() 海里后到达
海里后到达![]() ,此时,测得海岛
,此时,测得海岛![]() 在北偏东
在北偏东![]() 的方向上,要使船与海岛
的方向上,要使船与海岛![]() 最近,则船应继续向东前进________海里.
最近,则船应继续向东前进________海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 、
、![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万元购买
种型号电脑的数量与用8万元购买![]() 种型号电脑的数量相同.求
种型号电脑的数量相同.求![]() 、
、![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为12,点O为对角线AC、BD的交点,点E在CD上,tan∠CBE= ![]() ,过点C作CF⊥BE,垂足为F,连接OF,将△OCF绕着点O逆时针旋转90°得到△ODG,连接FG、FD,则△DFG的面积是________.
,过点C作CF⊥BE,垂足为F,连接OF,将△OCF绕着点O逆时针旋转90°得到△ODG,连接FG、FD,则△DFG的面积是________.
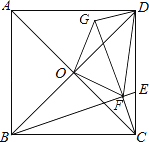
查看答案和解析>>
科目:初中数学 来源: 题型:
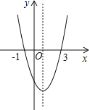
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .其中,正确的说法有________(请写出所有正确说法的序号).
.其中,正确的说法有________(请写出所有正确说法的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的是_____.
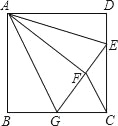
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com