Question

【题目】如图所示，E、F分别为线段AC上的两个点，且DE⊥AC于点E，BF⊥AC于点F，若AB=CD，AE=CF，BD交AC于点M．

(1)试猜想DE与BF的关系，并证明你的结论；

(2)求证：MB=MD．

Answer 1

【答案】（1）证明见解析 （2）证明见解析

【解析】

试题（1）根据BF⊥AC,DE⊥AC，AE=CF AF=AE+EF CE=CF+EF，可以证明Rt△ABF≌Rt△CDE，得DE=

BF；再根据BF⊥AC,DE⊥AC，可以证明DE//BF.（2）根据（1）中的结论，可证△BFM≌△DEM，从而证明MB=MD.

试题解析：（1）①DE与BF的关系可以有DE=BF成立，理由如下：

∵AE=CF AF=AE+EF CE=CF+EF

∴AF=CE 又∵BF⊥AC,DE⊥AC

∴∠BFA=∠DEC=90°

在Rt△ABF和Rt△CDE中

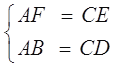
∴Rt△ABF≌Rt△CDE （HL）

∴DE=BF（全等三角形对应边相等）

②DE与BF的关系可以有DE//BF，理由如下：

∵DE⊥AC BF⊥AC

∴DE//BF

（2）证明：

∵Rt△ABF≌Rt△CDE

∴BF=ED

在△BFM和△DEM中

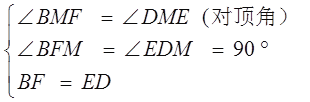
∴△BFM≌△DEM （AAS）

∴MB=MD