
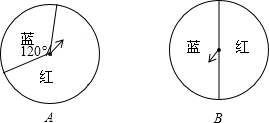
 游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A($\frac{3}{2}$,6),B(-3,0),C(6,0),点P在线段AB上,过点P作PQ∥x轴,交AC与点Q,设点P的纵坐标为m.
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A($\frac{3}{2}$,6),B(-3,0),C(6,0),点P在线段AB上,过点P作PQ∥x轴,交AC与点Q,设点P的纵坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又AP$\underset{∥}{=}$BE(点P、E在直线AB的同侧),如果BD=$\frac{1}{3}$AB,那么△PBC的面积与△ABC面积之比为2:3.
如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD、BF为邻边作平行四边形BDEF,又AP$\underset{∥}{=}$BE(点P、E在直线AB的同侧),如果BD=$\frac{1}{3}$AB,那么△PBC的面积与△ABC面积之比为2:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com