

分析 (1)延长BG交DE于点H,易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠DHB=90°;
(2)易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠BCD=90°.
解答 解:(1)延长BG交DE于点H,
在△BCG与△DCE中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠EDC,BG=DE,
∵∠BGC=∠DGH,
∴∠DHB=∠BCG=90°,
∴BG⊥DE;
(2)BG=DE,BG⊥DE仍然成立
如图2,∠BCD+∠DCG=∠ECG+∠DCG,
即∠BCG=∠DCE,
在△BCG与△DCE中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCG=∠DCE}\\{CG=CE}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠EDC,BG=DE,
∵∠BHC=∠DHG,
∴∠BCD=∠DOB=90°,
即BG⊥DE
点评 本题主要考查正方形,涉及正方形的性质,旋转的性质,全等三角形的判定与性质,综合程度较高,需要学生灵活所知识解答.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | |-4|=4 | B. | -|5|=-|-5| | C. | |-5|=|5| | D. | |-$\frac{1}{2}$|=-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
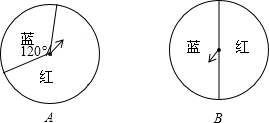 游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com