
 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A($\frac{3}{2}$,6),B(-3,0),C(6,0),点P在线段AB上,过点P作PQ∥x轴,交AC与点Q,设点P的纵坐标为m.
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A($\frac{3}{2}$,6),B(-3,0),C(6,0),点P在线段AB上,过点P作PQ∥x轴,交AC与点Q,设点P的纵坐标为m.分析 (1)设直线AB的函数解析式为y=kx+b,将A($\frac{3}{2}$,6),B(-3,0)代入函数解析式,解方程组即可.
(2)求出P、Q两点坐标,d=Q的横坐标-P的横坐标.
(3)分三种情形讨论①当MP=MQ,∠PMQ=90°时,点M在线段PQ的垂直平分线上,②当MP=PQ,∠MPQ=90时,③当MQ=PQ,∠PQM=90°时,列出方程求出m即可.
解答 解:(1)设直线AB的函数解析式为y=kx+b,
将A($\frac{3}{2}$,6),B(-3,0)代入函数解析式,得
$\left\{\begin{array}{l}{\frac{3}{2}k+b=6}\\{-3k+b=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=4}\end{array}\right.$,
直线AB的函数解析式为y=$\frac{4}{3}$x+4,
同理可求得直线AC的函数解析式为y=-$\frac{4}{3}x$+8,
(2)当y=m时,代入y=$\frac{4}{3}$x+4得x=$\frac{3}{4}$m-3,
即P($\frac{3}{4}$m-3,m),
当y=m时,代入y=-$\frac{4}{3}$x+8得x=-$\frac{3}{4}$m+6,
即Q(-$\frac{3}{4}$m+6,m),
∴d=PQ=-$\frac{3}{4}$m+6-($\frac{3}{4}$m-3)=-$\frac{3}{2}$m+9,
(3)①当MP=MQ,∠PMQ=90°时,点M在线段PQ的垂直平分线上,
∴线段PQ的中点坐标为($\frac{3}{2}$,m),
∴M($\frac{3}{2}$,0),
②当MP=PQ,∠MPQ=90时,由题意m=-$\frac{3}{2}$m+9,
∴m=$\frac{18}{5}$,
∴点P纵坐标为$\frac{18}{5}$,
∴$\frac{18}{5}$=$\frac{4}{3}$x+4,
∴x=-$\frac{3}{10}$,
此时点M(-$\frac{3}{10}$,0)
③当MQ=PQ,∠PQM=90°时,由②可知,点M的横坐标为$\frac{18}{5}$-$\frac{3}{10}$=$\frac{33}{10}$,
此时点M($\frac{33}{10}$,0)
综上所述点M1(-$\frac{3}{10}$,0)或M2($\frac{33}{10}$,0)或M3($\frac{3}{2}$,0).
点评 本题考查三角形综合题、一次函数的性质,解题的关键是求出关键点的坐标,学会分类讨论,学会把问题转化为方程解决,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | (1,-1) | B. | (3,-1) | C. | (3,-3) | D. | (3,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | |-4|=4 | B. | -|5|=-|-5| | C. | |-5|=|5| | D. | |-$\frac{1}{2}$|=-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24,△OAB的周长是18,试求EF的长.
如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24,△OAB的周长是18,试求EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,延长△ABC的边BC到点D,使CD=BC,延长边CA到点E,使AE=AC,延长AB到点F,使FB=AB,连接DE,FD,FE,得到△DEF,若S△EFD=168,则S△ABC为( )
如图,延长△ABC的边BC到点D,使CD=BC,延长边CA到点E,使AE=AC,延长AB到点F,使FB=AB,连接DE,FD,FE,得到△DEF,若S△EFD=168,则S△ABC为( )| A. | 42 | B. | 28 | C. | 24 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
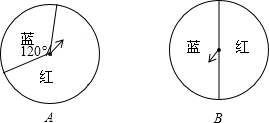 游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.
游戏者同时转动如图的两个转盘进行“配紫色游戏”,若要使游戏者获胜的概率为$\frac{1}{10}$,转盘B不动,转盘A应该如何设计?并写出解答过程说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com